Hi, Selamat datang di wikitanic.com.
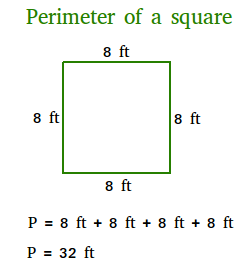
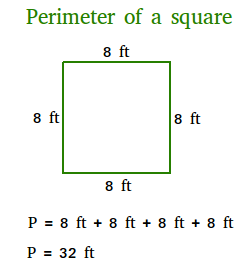
Keliling persegi adalah jarak keliling persegi. Dengan kata lain, keliling adalah jumlah panjang sisi-sisinya. Karena semua sisi persegi sama, Anda cukup mengalikan panjang salah satu sisinya dengan 4 untuk mendapatkan kelilingnya.
Penurunan rumus keliling persegi
Misalkan s adalah panjang salah satu sisi persegi dan misalkan P adalah kelilingnya. Berikut adalah cara mencari keliling (P) atau jarak keliling bagian luar persegi.
P = s + s + s + s = 4 × s
Oleh karena itu, rumus yang digunakan untuk mencari keliling persegi adalah P = 4 × s.
Perimeter dinyatakan dalam satuan.
- Jika s diukur dalam feet, maka keliling diukur dalam feet atau ft.
- Jika s diukur dalam sentimeter, maka keliling diukur dalam sentimeter atau cm.
- Jika s diukur dalam meter, maka keliling diukur dalam meter atau m.
Cara mencari keliling persegi
Itu semua tergantung pada informasi apa yang diberikan kepada Anda. Anda dapat menemukan keliling persegi menggunakan salah satu informasi berikut.
- Panjang satu sisi
- Luas alun-alun
- Diagonal persegi
Cara mencari keliling persegi menggunakan panjang salah satu sisi persegi
Contoh 1
Hitunglah keliling persegi jika s = 3 cm
P = 4 × s = 4 × 3 = 12 cm
Perhatikan bahwa tidak apa-apa untuk melakukan P = 3 + 3 + 3 + 3 = 12
Namun, biasanya lebih mudah dan lebih cepat untuk melakukan 4 kali 3 daripada menambahkan 3 empat kali.
Contoh #2
Temukan P ketika s = 5 cm
P = 4 × s = 4 × 5 = 20 cm
Contoh #3
Temukan P ketika s = 2/8 cm
P = 4 × s = 4 × 1/8
P = (4/1) × (2/8)
P = (4 × 2) / ( 1 × 8 ) = 8/8 = 1 cm
Cara mencari keliling persegi menggunakan luas persegi
Contoh #4
Luas sebuah persegi adalah 36 meter persegi. Berapakah keliling persegi tersebut?
Hal pertama yang harus dilakukan adalah mencari panjang sisi persegi dengan mengambil akar dari luasnya.
Rumus untuk mencari luas persegi adalah A = s2
Ganti 36 untuk A.
36 = s2
s = √(36)
s = 6
P = 4 × 6 = 24 meter
Cara mencari keliling persegi menggunakan panjang diagonal persegi
Contoh #5
Jika diagonal suatu persegi berukuran 2√2, tentukan kelilingnya.
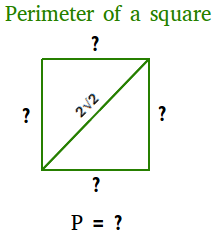
Perhatikan bahwa panjang diagonal adalah panjang sisi miring. Oleh karena itu, gunakan teorema Pythagoras untuk mencari panjang sisi persegi. Membiarkan s menjadi panjang salah satu sisi.
(2√2)2 = s2 + s2
22(√2)2 = 2s2
4(2) = 2s2
Bagilah kedua sisi dengan 2
4 = s2
s sama dengan akar kuadrat dari 4
s = 2
P = 4 × dtk
P = 4 × 2 = 8
Menemukan panjang sisi persegi ketika keliling diberikan
Contoh #6
Sebuah persegi memiliki keliling 12 cm. Temukan s
Di sini, dengan keliling persegi, Anda diminta untuk mencari panjang sisi persegi.
Kita tahu bahwa P = 4 × s
Anda harus mengganti P dengan 12 karena itulah yang mereka berikan kepada Anda.
Jadi, 12 = 4 × dtk
Masalahnya menjadi persamaan perkalian yang harus Anda pecahkan
Namun Anda dapat memecahkan persamaan ini dengan matematika mental. Ganti s dengan tanda tanya (?) dan tanyakan pada diri Anda hal berikut:
4 kali ? = 12 atau 4 kali apa yang akan memberi saya 12? Jawabannya adalah 3, jadi s = 3
Contoh #7
Keliling sebuah persegi adalah 64 cm. Berapakah panjang salah satu sisinya?
Sekali lagi, karena P = 4 × s, kita mendapatkan 64 = 4 × s setelah mengganti P dengan 64.
Tanyakan pada diri Anda 4 kali apa yang akan memberi saya 64? Karena 4 kali 16 adalah 64, s = 16
Anda juga dapat memecahkan persamaan untuk mencari s. Cukup bagi kedua sisi persamaan dengan 4.
64 = 4 × det
64/4 = (4 × det) / 4
16 = s
Faktanya, setiap kali Anda mencari s dan P adalah angka yang besar, Anda harus selalu membagi p dengan 4 untuk mendapatkan s.
Bisakah luas dan keliling persegi sama?
Tidak, itu tidak mungkin! Perimeter dinyatakan dalam unit. Namun, luas dinyatakan dalam satuan persegi atau satuan2
Karena itu, unit tidak pernah bisa sama dengan satuan2 sama seperti 4 tidak akan pernah sama dengan 42
Jika Anda mengukur keliling kebun Anda, bisa jadi sama dengan keliling kebun orang lain.
Jika Anda mengukur luas taman Anda, bisa jadi sama dengan luas taman orang lain.
Namun, tidak masuk akal untuk mengatakan bahwa keliling taman Anda bisa sama dengan luas taman orang lain.
Namun, jika Anda ingin mengabaikan semua logika dan fakta bahwa mereka tidak bisa sama, Anda bisa membiarkan s2 = 4s dan lihat apa yang Anda dapatkan untuk s.
s2 = 4s
s2 – 4s = 0
s(s – 4) = 0
s = 0 dan s = 4
P = 4s = 4(4) = 16 satuan
A = s2 = 42 = 4(4) = 16 satuan2
Namun, 16 unit tidak sama dengan 16 unit2