Hey, Selamat datang di wikitanic.com.
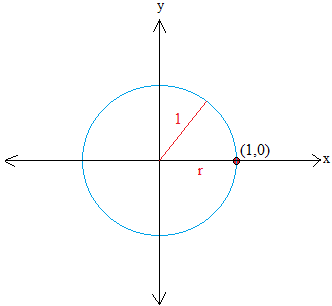
Lingkaran satuan adalah lingkaran yang jari-jarinya sama dengan 1. Selanjutnya lingkaran tersebut berpusat pada titik asal sistem koordinat segi empat.
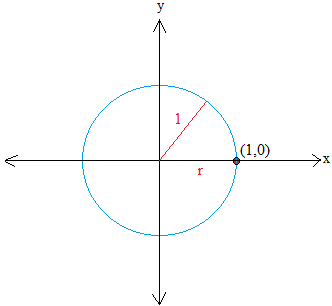
Misalkan P = (x , y) adalah titik pada lingkaran. Kemudian, buat segitiga siku-siku dengan menggambar garis tegak lurus x. Garis ditunjukkan dengan warna hijau.
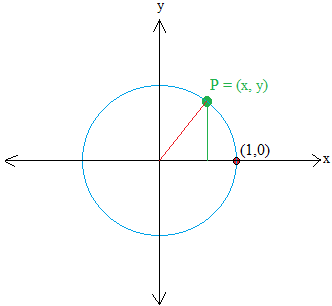
Kaki horizontal segitiga berjarak x satuan dari titik asal dan kaki vertikal segitiga berjarak y satuan dari titik asal.
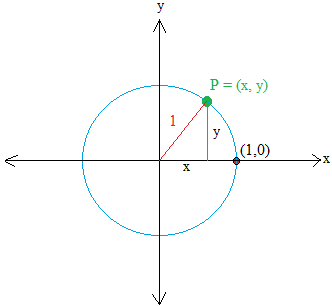
Menggunakan teorema Pythagoras, kita mendapatkan x2 + y2 = 12 atau x2 + y2 = 1
Kita dapat melangkah lebih jauh sehingga kita dapat memperoleh fungsi trigonometri yang penting. Mari kita beri nama θ sudut yang dibuat dengan jari-jari berwarna merah dan sumbu x.
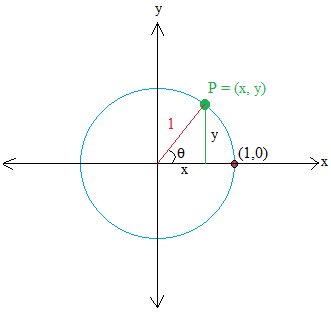
Perhatikan baik-baik segitiga tersebut dan Anda akan melihat seperti yang telah kita pelajari sebelumnya bahwa sisi yang berdekatan dengan sudut θ adalah x dan sisi yang berlawanan adalah y.
Oleh karena itu, sinθ = y / 1 = y dan cosθ = x / 1 = x
sinθ dibaca sebagai sinus dari θ dan sinθ adalah koordinat y dari titik P.
cosθ dibaca sebagai cosinus dari θ dan cosθ adalah koordinat x dari titik P.
Kita dapat mengganti x = cosθ dan sinθ di x2 + y2 = 1
Kita dapatkan (cosθ)2 + (sinθ)2 = 1 atau cos2θ + dosa2θ = 1
Definisi dari enam fungsi trigonometri dalam hal lingkaran satuan.
cosθ = x
secθ = 1/x, dengan x tidak sama dengan 0 (secθ adalah kebalikan dari cosθ)
sinθ = dan
cscθ = 1/y, dengan y tidak sama dengan 0 (cscθ adalah kebalikan dari sinθ)
tanθ = y/x, dengan x tidak sama dengan 0
cotθ = x/y, dengan y tidak sama dengan 0 (cotθ kebalikan dari tanθ)
Kita juga dapat memanggil enam fungsi trigonometri di atas fungsi lingkaran karena kita menggunakan lingkaran satuan untuk menyatakan nilai fungsi.
Kami baru saja menurunkan beberapa fungsi trigonometri yang paling penting. Kami baru saja menggores permukaan dari apa yang bisa kami lakukan dengan lingkaran unit. Sekarang kita perlu melengkapi lingkaran satuan dengan nilai trigonometri yang paling penting
Cara mencari nilai trigonometri menggunakan lingkaran satuan
Dua pelajaran menggunakan lingkaran satuan untuk menemukan sin(45 derajat) dan cos(45 derajat) dan menggunakan lingkaran satuan untuk menemukan kosinus dan sinus sudut 30 dan 60 derajat akan menunjukkan bagaimana Anda dapat menggunakan lingkaran satuan untuk menemukan yang berikut ini nilai trigonometri yang penting.
- sin 45 derajat = √(2) / 2
- cos 45 derajat = √(2) / 2
- cos(30 derajat) = √3 / 2
- sin(60 derajat) = √3 / 2
Karena nilai di atas adalah bilangan positif, mereka akan berada di kuadran pertama lingkaran satuan. Kami juga akan menempatkan setiap nilai pada lingkaran satuan sebagai titik (x, y).
Ingat bahwa dari bagian sebelumnya, kita melihat bahwa cosθ = x dan sinθ = y
(x, y) = (cosθ, sinθ)
Anda kemudian akan memiliki titik-titik ini di kuadran pertama.
- (cos 30 derajat, sin 30 derajat) = (√3 / 2, 1 / 2)
- (cos 45 derajat, sin 45 derajat) = (√2 / 2, √2 / 2)
- (cos 60 derajat, sin 60 derajat) = (1/2, √3/2)
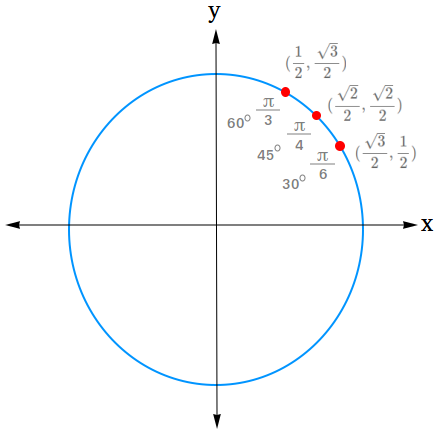
Perhatikan bahwa dalam radian,
30 derajat sama dengan π/6 rad
45 derajat sama dengan π/4 rad
60 derajat sama dengan π/3 rad
Sekarang, kita perlu menemukan lebih banyak nilai trigonometri di kuadran II, kuadran III, dan kuadran IV.
Kuadran II
Titik-titik di kuadran kedua yang kita cari akan simetris dengan tiga titik di kuadran pertama terhadap sumbu y. Nilai y positif, tetapi nilai x negatif.
Titik simetris 60 derajat memiliki sudut sebesar 120 derajat (60 + 30 + 30)
Titik simetris 45 derajat memiliki sudut sebesar 135 derajat (45 + 45 + 45)
Titik simetris 30 derajat memiliki sudut sebesar 150 derajat (30 + 30 + 30 + 30 + 30)
Anda kemudian akan memiliki titik-titik ini di kuadran kedua.
- (cos 120 derajat, sin 120 derajat) = (-1/2, √3/2)
- (cos 135 derajat, sin 135 derajat) = (-√2 / 2, √2 / 2)
- (cos 150 derajat, sin 150 derajat) = (-√3 / 2, 1/2)
Kuadran III
Titik-titik di kuadran ketiga simetris dengan tiga titik di kuadran kedua terhadap sumbu x. Nilai y negatif dan nilai x negatif.
Titik simetris 120 derajat memiliki sudut sebesar 240 derajat (120 + 60 + 60)
Titik simetris 135 derajat memiliki sudut sebesar 225 derajat (135 + 45 + 45)
Titik simetris 150 derajat memiliki sudut sebesar 210 derajat (150 + 30 + 30)
Anda kemudian akan memiliki titik-titik ini di kuadran ketiga.
- (cos 240 derajat, sin 240 derajat) = (-1 / 2, -√3 / 2)
- (cos 225 derajat, sin 225 derajat) = (-√2 / 2, -√2 / 2)
- (cos 210 derajat, sin 210 derajat) = (-√3 / 2, -1 / 2)
Kuadran IV
Titik-titik di kuadran keempat simetris dengan tiga titik di kuadran ketiga terhadap sumbu y. Nilai y negatif dan nilai x positif.
Titik simetris 240 derajat memiliki sudut sebesar 300 derajat (240 + 30 + 30)
Titik simetris 225 derajat memiliki sudut sebesar 315 derajat (225 + 45 + 45)
Titik simetris dengan 210 derajat memiliki sudut yang sama dengan 330 derajat (210 + 60 + 60)
Anda kemudian akan memiliki titik-titik ini di kuadran keempat.
- (cos 300 derajat, sin 300 derajat) = (1/2, -√3/2)
- (cos 315 derajat, sin 315 derajat) = (√2 / 2, -√2 / 2)
- (cos 330 derajat, sin 330 derajat) = (√3 / 2, -1 / 2)
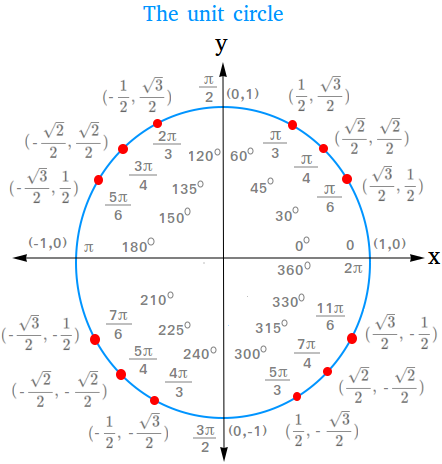
Satuan lingkaran dan Nilai trigonometri