Halo, Selamat datang di wikitanic.com.
Kapan 144 lebih dekat ke 8 daripada ke 143?
Definisi biasa dari norma dari bilangan real adalah modulus atau nilai absolutnya
. Kami mengukur “jarak” antara dua bilangan real dengan menggunakan nilai absolut dari selisihnya. Ini memberikan metrik Euclidean
dan, dengan menggunakannya, kita dapat mendefinisikan topologi biasa pada bilangan real
.
Susunan standar bilangan real pada suatu garis secara otomatis memastikan bahwa bilangan dengan perbedaan Euclidean kecil di antara mereka secara geometris dekat satu sama lain. Mungkin mengejutkan bahwa ada cara lain untuk mendefinisikan norma dan jarak, yang menyediakan topologi lain, membawa kita ke konsep kedekatan yang sangat berbeda, dan ke sistem bilangan yang benar-benar baru, bilangan p-adic.
Penilaian 2-adik
Itu -adic penilaian – atau
-adic order (Katok, 2007) — bilangan bulat
adalah fungsinya
Dengan kata lain, the -penilaian adik dari
adalah indeks kekuatan terbesar dari
yang membagi
.
Kami akan prihatin secara eksklusif dengan kasus ini . “Tingkat kemerataan” suatu angka dapat dinyatakan dalam penilaian 2-adik. Untuk bilangan bulat
penaksiran 2-adik adalah bilangan asli terbesar
seperti yang
membagi
. Biasanya ditulis
. Untuk bilangan bulat genap,
. Dengan perjanjian,
(karena nol habis dibagi oleh setiap pangkat dari
).
Penilaian dapat diperluas ke bilangan rasional :
Dengan mudah dibuktikan bahwa, untuk setiap dua bilangan rasional, dan
,
yang seperti itu
dengan persamaan memegang jika . Ini dikenal sebagai pertidaksamaan segitiga yang kuat. Ini memiliki beberapa konsekuensi yang mengejutkan, salah satunya adalah, dalam geometri ini, semua segitiga adalah sama kaki!
Kami mencatat bahwa konsep “kedekatan” di bawah norma 2-adik sama sekali berbeda dengan konsep kedekatan yang biasa. Misalnya, selisih Euclidean antara dua bilangan 3 dan 8 adalah 5, karena . Tapi kita punya
. Memang, semua angka ganjil berada pada jarak satuan dari 8. Lebih aneh lagi, kita punya
sehingga 144 lebih dekat ke 8 daripada 143. Butuh beberapa waktu untuk membangun intuisi tentang hal ini, tetapi evaluasi p-adic adalah sekutu yang kuat dalam teori bilangan.
Jarak 2-adik antar angka
Kita dapat menggunakan norma 2-adik untuk menentukan jarak antara dua bilangan rasional. Untuk kesederhanaan, kami akan membatasi perhatian di bawah pada bilangan bulat, meskipun gagasannya lebih umum.
Jarak 2-adik antara dua bilangan asli dan
tertulis
didefinisikan sebagai
di mana
adalah penilaian 2-adik dari perbedaan antara angka-angka. Dia kebalikan dari pangkat terbesar dari 2 yang membagi selisihnya. Itu selalu membutuhkan salah satu nilai
.
Pada Gambar di sini, kami menunjukkan 32 bilangan asli pertama. Mempertimbangkan seluruh himpunan bilangan bulat kami hanya dapat menjamin bahwa dua bilangan bulat arbitrer berbeda dengan kelipatan
jadi jarak maksimumnya adalah
. Jadi, semua angka yang ditunjukkan pada gambar — dan memang semua bilangan bulat — memiliki jarak paling banyak
dari satu orang ke orang lainnya.
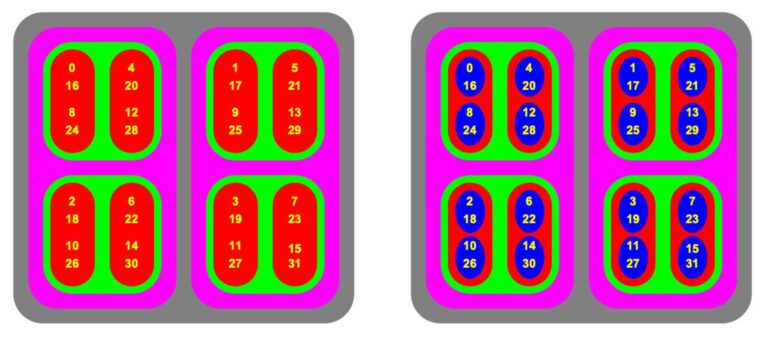
Pada gambar di bawah (panel kiri) kita pisahkan angka menjadi paritas genap dan paritas ganjil. Dalam masing-masing dari dua himpunan ini, setiap dua angka selalu berbeda dengan angka genap, sehingga jarak 2-adik selalu paling banyak . Dengan demikian, angka di salah satu wilayah magenta lebih dekat satu sama lain daripada dua angka dengan satu angka di setiap wilayah.

Kiri: angka dalam wilayah magenta berbeda dengan kelipatan 2. Kanan: angka dalam wilayah hijau berbeda dengan kelipatan 4.
Pada gambar (panel kanan), kami memisahkan angka menjadi empat set, di mana semua angka berbeda dengan kelipatan 4. Jadi, dua angka dalam satu wilayah hijau paling banyak berbeda . Jarak antar angka di wilayah hijau yang berbeda setidaknya
.
Melanjutkan proses, semua angka dalam satu wilayah merah pada gambar di bawah (panel kiri) berbeda dengan kelipatan 8 dan jarak satu sama lain paling banyak .
Akhirnya, semua angka dalam wilayah biru pada gambar (panel kanan) berbeda dengan kelipatan 16 dan jarak satu sama lain paling banyak .

Kiri: angka dalam wilayah merah berbeda dengan kelipatan 8. Kanan: angka dalam wilayah biru berbeda dengan kelipatan 16.
Tutup Bola
Bilangan p-adik didefinisikan dengan membentuk penutupan bidang bilangan rasional dalam topologi yang timbul dari metrik p-adic. Kami tidak akan membahas ini (lihat Katok, 2007) tetapi kami akan mempertimbangkan bola terbuka dan tertutup yang ditentukan untuk metrik ini. Bola terbuka
adalah himpunan titik-titik yang p-adic jarak dari
kurang dari
:
Ternyata itu keduanya terbuka dan tertutup: itu adalah a set tutup. Yang lebih menarik adalah bahwa setiap titik bola adalah pusatnya:
Daerah berwarna yang telah kami tunjukkan pada gambar di atas adalah bola terbuka (tentu saja, kami hanya menyertakan sejumlah kecil elemen). Misalnya, area abu-abu adalah ; area merah kanan atas adalah
dan wilayah biru kanan bawah adalah
.
Lebih Banyak Visualisasi
Ada banyak cara lain untuk menggambarkan bilangan rasional untuk menekankan sifat-sifat seperti jarak (Lynch dan Mackey, 2022). Dengan sedikit keahlian grafis, kami dapat menyusun angka-angka di atas dalam menara vertikal, dengan koordinat vertikal menjadi penilaian 2-adik untuk wilayah terdalam.
Ilustrasi di bawah ini, menunjukkan menara fraktal dari angka 3-adik, berasal dari artikel terbaru di Kuanta Majalah (Houston-Edwards, 2020). Diagram serupa dapat dibuat untuk bilangan p-adik dengan bilangan prima lainnya (lihat Katok, 2007).

Visualisasi angka 3-adik [Image: Samuel Velasco/Quanta Magazine].
Sumber
Katok, Svetlana, 2007: pAnalisis -adic Dibandingkan dengan Nyata. Matematika Siswa. Lib., Vol. 37. Amer. Matematika. Soc., ISBN: 978-0-8218-4220-1.
Kelsey Houston-Edwards, 2020: Semesta Sistem Bilangan Tak Terbatas. Majalah Quanta19 Oktober 2020. LINK.
Lynch, Peter & Michael Mackey, 2022: Paritas dan Partisi Bilangan Rasional. arXiv.
Artikel Wikipedia: Nomor p-adik.