Kurva spiral dan potret fase

Halo, Selamat datang di wikitanic.com.

Kiri: Bagian berbentuk kerucut. Kanan: bagian Spiric [images Wikipedia Commons].

Kita sangat mengenal bagian kerucut, yaitu kurva yang terbentuk dari perpotongan bidang dengan kerucut. Ada keluarga kurva lainnya, yaitu Bagian spirik, dibentuk oleh perpotongan torus dengan bidang yang sejajar dengan sumbunya. Seperti kerucut, bentuknya bermacam-macam, bergantung pada jarak bidang dari sumbu torus (lihat Gambar di atas). Kami memeriksa bagaimana kurva spiral dapat ditemukan dalam ruang fase dari sistem dinamik.

Koordinat di Torus

Sebuah torus (Yunani $\math\sigma\pi\epsilon\iota\rho\alpha$ torus) dapat dianggap sebagai produk dari dua lingkaran, $S^1\kali S^1$ . Bagian spirik adalah perpotongan bidang yang sejajar dengan sumbu torus. Posisi pada torus dapat ditentukan oleh toroidal dan poloidal koordinat. Komponen toroidal ( $\lambda$ ) adalah sudut yang mengikuti lingkaran besar di sekitar torus. Hal ini analog dengan bujur, bervariasi sepanjang kesejajaran. Koordinat poloidal ( $\theta$ ) bervariasi sepanjang lingkaran yang lebih kecil di sekitar permukaan; berubah $\theta$ seperti mengubah garis lintang. Kedua parameter mengambil semua nilai dalam rentang $[0,2\pi)$ .

The equations in cartesian coordinates for a point on the torus with toroidal/poloidal coordinates $(\lambda,\theta)$ are given by

$\displaystyle \beginarrayrcl x &=& (R + a \cos\theta )\cos\lambda \\ y &=& (R + a \cos\theta )\sin\lambda \\ z &=& a \sin\theta \endarray$

(we assume $a<R$ ). Suppose we take the plane $y=y_0$ or — using the parametric equations — $(R + a\cos\theta)\sin\lambda=y_0$ . Substituting this into the other equations, we get a quartic relationship between $x$ and $z$ :

$\displaystyle [(x^2+z^2)-(R^2+a^2-y_0^2)]^2 = 4R^2(a^2-z^2)\,.$

Kurva ini dikenal sebagai bagian spiric Perseus. Hampir tidak ada yang diketahui tentang Perseus, kecuali bahwa dia aktif pada abad kedua SM. Proclus (411–485 M) menulis bahwa Perseus diasosiasikan dengan kurva spiral dengan cara yang sama seperti Apollonius diasosiasikan dengan kerucut. Bagian spiral termasuk oval Cassini sebagai kasus khusus. Satu set kurva tersebut ditunjukkan pada Gambar di bawah ini.

Bagian spiral: persimpangan antara torus dan bidang yang sejajar dengan sumbunya.

Pada Gambar di bawah ini, kami memplot kurva spirik untuk mencegat nilai dalam kisaran $y_0\in\0.0,0.9,1.0,1.1,1.3,2.0,2.5,2.95\$ dengan nilai parameter $R=2$ dan $a=1$ . Dalam kasus yang membatasi $y_0=0$ , spiric terdiri dari dua lingkaran. Sebagai $y_0$ meningkat, ini terdistorsi dan kapan $y_0=1.0$ , mereka bergabung menjadi satu kurva, lemniscate of Bernoulli. Sebagai $y_0$ tumbuh lebih jauh, ini menjadi berbentuk kacang dan kemudian menjadi oval cembung sebelum mengecil ke suatu titik ketika $y_0 = 3$ .

Kurva spiral untuk nilai parameter $y_0\in\0.0,0.9,1.0,1.1,1.3,2.0,2.5,2.95\$ .

Perspektif lain

Sangat mencerahkan untuk memplot spirik sebagai fungsi dari koordinat toroidal dan poloidal. Kami melakukan ini pada gambar berikut. Gambar simetris tentang vertikal melalui $\lambda=\pi$ . Dua kurva yang sesuai dengan lemniscate diplot dengan warna merah.

Kurva spiral di ( $\lambda,\theta$ )-spasi, untuk $y_0\in\ 0,0, 0,25, 0,5, 1,0, 1,5, 2,0, 2,5, 2,95 \$ .

Kiri: Kurva spiral di ( $\lambda,\theta$ )-spasi, untuk $y_0\in\ 0,0, 0,25, 0,5, 1,0, 1,5, 2,0, 2,5, 2,95 \$ . Kanan: bidang fase untuk bandul sederhana.

Pada gambar di atas, kami mengganti koordinat $\lambda$ dan $\theta$ (panel kiri). Di panel kanan kami menampilkan potret fase untuk pendulum sederhana. Kemiripan antara kedua plot itu jelas. Untuk pendulum, setiap kurva mewakili tingkat energi tertentu. Karena energi dilestarikan, lintasan dalam ruang fase terletak pada permukaan energi konstan.

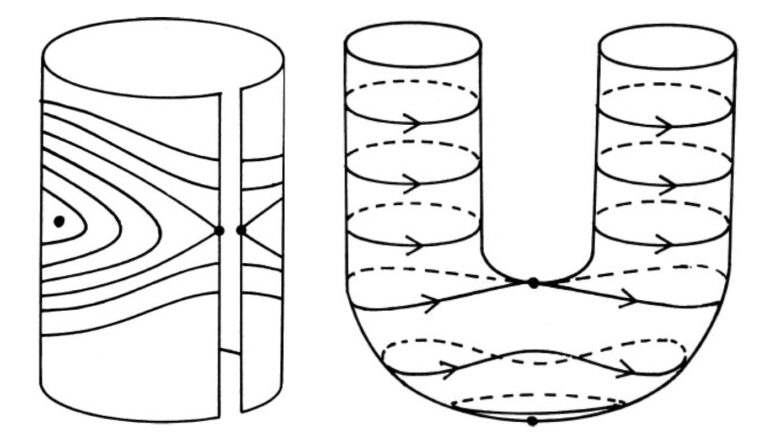
Kiri: Bidang fase dibungkus menjadi silinder. Kanan: Silinder bengkok menjadi tabung. Ketinggian kurva sesuai dengan energi [Figures from Stewart (1997)].

Representasi gerak yang cerdas, dengan energi sebagai koordinat vertikal, dibahas dalam buku Ian Stewart Apakah Tuhan Memainkan Dadu? Pada gambar di atas, plot fase bandul sederhana digulung menjadi silinder (panel kiri) dan silinder ini kemudian ditekuk menjadi permukaan berbentuk U (panel kanan). Di panel kanan, lintasan ditemukan pada level vertikal tetap (energi tetap). Kita dapat melihat bagaimana kurva ini tampak mirip dengan kurva bagian spirik yang diplot di atas.

Akan menarik untuk mempertimbangkan sifat dari sistem dinamik yang lintasannya adalah kurva spiral.

Sumber

$\peluru$ Stewart, Ian, 1997: Apakah Tuhan Memainkan Dadu? Matematika Kekacauan Baru. Penguin Inggris. ISBN: 9780141928074.

$\peluru$ artikel Wikipedia Bagian Spirik: Wiki

Leave a Comment Cancel reply