Hello, Selamat datang di wikitanic.com.
 Awal topologi sering ditelusuri ke solusi teka-teki Euler, Jembatan Königsberg. Masalah yang ditimbulkan adalah mengikuti jalan melalui kota Prusia yang melintasi ketujuh jembatan tepat satu kali.
Awal topologi sering ditelusuri ke solusi teka-teki Euler, Jembatan Königsberg. Masalah yang ditimbulkan adalah mengikuti jalan melalui kota Prusia yang melintasi ketujuh jembatan tepat satu kali.
Euler membuktikan bahwa masalahnya tidak ada solusinya. Dia secara drastis menyederhanakannya dengan mengganti konteks geografis dengan grafik sederhana dengan simpul untuk setiap daratan dan tepi untuk setiap jembatan.

Masalah Jembatan Königsberg. Kiri: peta kasar topografi kota. Kanan: representasi sebagai grafik sederhana.
Permata Euler
Hasil umum yang luar biasa ditemukan oleh Euler. Untuk grafik bidang apa pun, jika ,
Dan
adalah jumlah simpul, sisi, dan sisi, maka
Ini adalah kasus khusus dari hasil yang jauh lebih umum. Ini juga berlaku untuk polihedra dalam ruang 3 dan untuk politop dalam ruang berdimensi lebih tinggi. Penjelasan yang sangat bagus tentang apa yang disebut ‘Permata Euler’ diberikan dalam buku David Richeson (2008).
Dalam kasus masalah jembatan, kita punya ,
Dan
(kami menghitung wilayah luar sebagai wajah). Tentu saja, Permata Euler puas:
.
Jalur dan Sirkuit Euler
Lintasan Euler adalah lintasan yang melintasi setiap sisi tepat satu kali. Sirkuit Euler adalah lintasan Euler yang berawal dan berakhir pada simpul yang sama. Konsep ini pertama kali dipertimbangkan oleh Leonhard Euler 1n 1736, sehubungan dengan masalah Tujuh Jembatan Königsberg.
Derajat suatu simpul adalah jumlah sisi yang terhubung dengannya. Euler membuktikan bahwa syarat yang diperlukan untuk keberadaan sirkuit Euler adalah bahwa semua simpul dalam grafik memiliki derajat genap. Hasil ini sekarang dikenal sebagai Teorema Euler: Graf terhubung memiliki sirkuit Euler jika dan hanya jika setiap simpul berderajat genap.

Kiri: Grafik Euler, representasi sederhana dari masalah Jembatan Königsberg. Tengah: Ganda dari grafik Euler. Kanan: Superposisi grafik dan dual.
Hasil Euler mudah dipahami: pada jalur Euler, setiap tautan ‘masuk’ di sebuah simpul harus memiliki tautan ‘keluar’ yang sesuai. Dengan demikian, jumlah total tautan harus genap, atau derajat simpulnya harus genap. Menghitung sisi-sisi yang terhubung ke setiap simpul dalam grafik Euler (Gambar di atas, panel kiri), kami menemukan bahwa tiga simpul memiliki derajat 3 sedangkan satu simpul memiliki derajat 5.
Jalur dan Sirkuit Hamiltonian
Lintasan Hamiltonian adalah lintasan yang mengunjungi setiap simpul tepat satu kali. Sirkuit Hamiltonian adalah lintasan Hamiltonian yang berawal dan berakhir pada simpul yang sama (merupakan sirkuit tertutup). Graf yang memuat sirkuit hamiltonian disebut graf hamiltonian.
Jelas, grafik Königsberg Euler adalah grafik Hamiltonian: dengan menelusuri jalur tertutup di sekitar tepi luar, kami melewati semua simpul dan kembali ke titik awal.
Grafik Ganda
Untuk setiap graf bidang di dalam bidang, ada graf lain yang disebut dualnya. Graf ganda memiliki simpul untuk setiap sisi dari graf asli dan sisi untuk setiap pasangan sisi yang dipisahkan oleh sisi. Ketika wajah yang sama muncul di kedua sisi sebuah sisi, graf ganda tersebut memiliki loop sendiri, sebuah sisi yang menghubungkan sebuah simpul ke dirinya sendiri.
Seringkali ada banyak representasi grafik yang berbeda di bidang. Meskipun jelas berbeda, mereka setara secara topologi. Pada gambar di bawah ini kami menunjukkan dua representasi graf ganda untuk Masalah Jembatan Königsberg. Keduanya homeomorfik dengan grafik di panel tengah Gambar di atas. Semua punya .

Dua lagi representasi graf ganda untuk Masalah Jembatan Königsberg. Kiri: Pentagon dengan dua diagonal. Kanan: Lingkaran dan dua akord.
Grafik Dipol dan Grafik Siklus
Grafik siklus adalah grafik yang terdiri dari satu siklus, sejumlah simpul yang terhubung dalam rantai tertutup. Urutan- grafik siklus, dengan
simpul, dilambangkan
. Jumlah simpul di
sama dengan jumlah sisi. Setiap simpul berderajat 2: setiap simpul memiliki tepat dua sisi yang terhubung dengannya. Kami bisa mewakili
oleh lingkaran dengan
titik-titik yang diidentifikasi sebagai simpul. Ini secara topologi setara dengan N-gon.

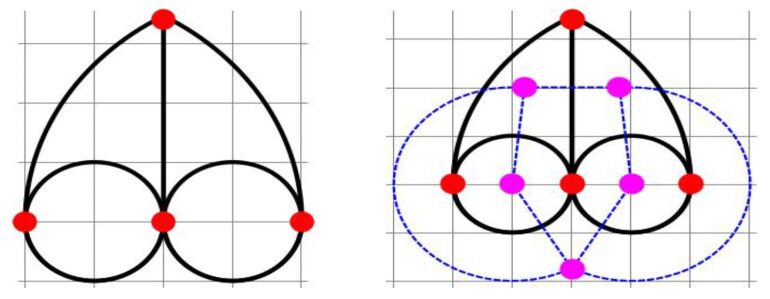
Kiri: Grafik dipol orde 7. Kanan: Grafik dan dualnya, grafik siklus orde-7 (biru).
Grafik dipol terdiri dari dua simpul yang dihubungkan oleh dua sisi atau lebih. Sebuah perintah- graf dipol memiliki n sisi, dilambangkan dengan
.
Grafik ganda pesanan- dipol adalah grafik siklus
. Ini terlihat jelas dari gambar di atas, di mana grafik dipol berwarna merah dan hitam sedangkan dual berwarna biru dan magenta. Sedangkan graf dipol orde-7 memiliki
grafik ganda memiliki
. Secara alami, keduanya memenuhi formula Permata Euler,
.
Kata penutup
Konsep grafik ganda berharga dalam banyak konteks. Ada banyak teorema tentang graf dan dualnya. Sebagai contoh, hasil standar teori graf menyatakan bahwa graf planar terhubung adalah Euler jika dan hanya jika graf rangkapnya adalah bipartit.
Dualitas relevan dalam konteks yang lebih luas daripada grafik planar dan telah dipelajari selama berabad-abad. Dualitas polyhedra cembung diakui oleh Johannes Kepler dalam bukunya tahun 1619 Harmoni Dunia.
Di postingan mendatang, kita akan melihat Tonnetz, representasi grafis dari nada-nada dalam tangga nada kromatik dan — melalui rangkapnya — hubungan antara sepertiga mayor dan akord lainnya.
Sumber
Richeson, David S., 2008: Permata Euler: Rumus Polihedron dan Kelahiran Topologi. Universitas Princeton. Tekan, 317pp. ISBN: 978-0-691-12677-7.
Itu Matematika, 7 November 2013: Permata Euler. DI SINI.