Kelengkungan dan Geodesik pada Torus

Hello, Selamat datang di wikitanic.com.

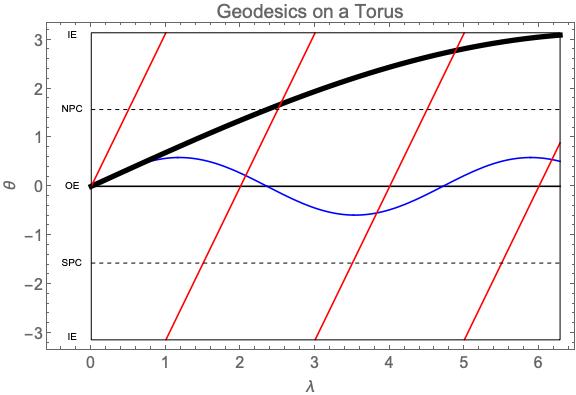
Geodesik pada torus [image from Jantzen, Robert T., 2021].

Kami melihat kelengkungan pada torus, dan berbagai bentuk yang dimiliki geodesik. Ini dibandingkan dengan geodesik pada “torus datar”.

Koordinat Toroidal-Poloidal

Posisi pada torus dapat ditentukan oleh koordinat toroidal dan poloidal. Komponen toroidal ( $\lambda$ ) adalah sudut yang mengikuti lingkaran besar di sekitar torus. Hal ini analog dengan bujur, bervariasi sepanjang kesejajaran. Koordinat poloidal ( $\theta$ ) bervariasi sepanjang lingkaran yang lebih kecil di sekitar permukaan. Mengubah $\theta$ seperti mengubah garis lintang. Kami ambil $\lambda\in[02\pi)[02\pi)}$ dan $-\pi\le\theta<\pi$ .

Kita dapat memetakan torus ke sebuah bidang dengan memotongnya sepanjang paralel terdalam dan membukanya rata. Jelas, ini melibatkan peregangan; pemetaannya bukan isometri. Kami mencatat beberapa kesejajaran tertentu: ekuator luar (OE) adalah paralel terpanjang; ekuator dalam (IE) adalah yang terpendek; lingkaran kutub utara (NPC) dan lingkaran kutub selatan (SPC) adalah paralel di bagian atas dan bawah torus. Perhatikan bahwa pada gambar di atas, sisi kiri dan kanan ( $\lambda=0$ dan $\lambda=2\pi$ ) harus diidentifikasi dan juga batas atas dan bawah ( $\theta=-\pi$ dan $\theta=\pi$ ).

Metrik dan Kelengkungan

Koordinat kartesius untuk suatu titik pada torus dengan koordinat toroidal/poloidal $(\lambda,\theta)$ diberikan oleh

$\displaystyle \beginarrayrcl x &=& (R + r \cos\theta )\cos\lambda \\y &=& (R + r \cos\theta )\sin\lambda \\z& = & r \sin\theta\,. \endarray$

Vektor posisi suatu titik pada permukaan adalah

$\displaystyle \mathbfx(\lambda,\phi) = \lengle (R + r \cos\theta )\cos\lambda, (R + r \cos\theta)\sin\lambda, r \sin\theta \rangle$

Vektor tangen dalam arah toroidal dan poloidal adalah

$\displaystyle \beginarrayrcl\mathbfe_\lambda = \frac\partial\mathbfx\partial\lambda &=& (-(R + r \cos\theta ) \sin\lambda, (R + r \cos\theta)\cos\lambda, 0 ) \\ \mathbfe}\theta = \frac\partial\mathbfx\partial\theta & =& ( r \sin\theta\cos\lambda, r \cos\theta\sin\lambda, 0 ) \,. \endarray$

Dari ini, koefisien metrik $g_ij = \mathbfe_i\mathbf\cdot e_j$ mengikuti:

$\displaystyle g_11 = (R + r \cos\theta )^2 \qquad g_12 = g_21 = 0 \qquad g_22 = r^2 \,.$

Dengan demikian kita dapat menuliskan persamaan untuk elemen garis:

$\displaystyle \mathrmds^2 = g_\mu\nu \mathrmdx^\mu \mathrmdx^\nu = (R + r \cos\theta )\mathrmd \lambda + r^2\mathrmd\theta\,.$

Sekarang mudah untuk menghitung simbol Christoffel dan tensor kelengkungan Riemann $R^\kappa_\lambda\mu\nu$ kontrakkan untuk mendapatkan tensor Ricci $R_\mu\nu$ dan kelengkungan Ricci $R$ , dari mana kelengkungan gaussian mengikuti. Semua ini dapat dilakukan dengan perangkat lunak sumber terbuka.

Untuk permukaan dua dimensi, kesimetrian tensor kelengkungan Riemann menyiratkan bahwa hanya ada satu komponen independen, yang kita bawa ke $R_1212$ . Ini ternyata

$\displaystyle R_1212 = - r\cos\theta(R + r\cos\theta)$

dan itu terkait dengan kelengkungan gaussian oleh $K = - R_1212/ \detg$ . Sebagai konsekuensi,

$\displaystyle K = \frac\cos\theta r(R+r\cos\theta) \,.$

Karena kami menganggap itu $r <R$ kelengkungan gaussian positif untuk ${|\theta|<\pi/2}$ dan negatif untuk $-\pi<\theta<-\pi/2$ dan $\pi/2<\theta<\pi$ . Ini masuk akal: kelengkungannya positif di luar torus dan negatif di dalam.

Kita dapat menulis persamaan untuk geodesik. Dalam bentuk umum, mereka

$\displaystyle \frac\mathrmd^2 x^\alpha\mathrmds^2 + \Gamma^\alpha_\mu\nu x^\mu x^\nu = 0 \ ,.$

Mengingat posisi dan kemiringan awal, ini dapat diselesaikan, secara analitis atau numerik. Satu-satunya paralel yang geodesik adalah ekuator luar (OE) dan ekuator dalam (IE). Semua meridian ( $\lambda$ konstan) adalah geodesik.

Kami menunjukkan beberapa tipikal geodesik pada gambar di atas; semua dimulai dari posisi $\lambda=\theta=0$ . Ada dua keluarga kurva generik. Untuk kurva yang tidak melewati lubang pusat, sudut poloidal dibatasi, $\dan\theta_b<\pi$ . Ini diwakili oleh kurva biru. Geodesik yang melewati lubang pusat diwakili oleh kurva merah; untuk ini, sudut poloidal bervariasi secara monoton. Keluarga dipisahkan oleh geodesik khusus yang mendekati ekuator dalam secara asimtotik (kurva hitam tebal).

Torus Datar

Jika kita menganggap itu $R$ besar dan $r=O(1)$ kelengkungan $K \kira-kira \cos\theta/(rR)$ kecil. Mempertahankan bentuk topologi torus tetapi mengatur kelengkungan ke nol, kita mendapatkan torus datar. Jelas bahwa semua geodesik pada torus datar adalah garis lurus. Semua paralel dan semua meridian adalah geodesik (garis horizontal dan vertikal pada diagram). Geodesik melalui asalnya adalah $\theta = m\lambda$ . Jika $m=r/s$ rasional, maka $r\lambda = s\theta$ dan geodesik menutup dengan sendirinya — bersifat periodik. Jika $m$ tidak rasional, geodesik menutupi torus dengan padat. Kurva periodik adalah simpul toroidal. Mereka dapat diidentifikasi dengan angka $(r,s)$ yang memberikan jumlah loop di sekitar sirkuit “panjang” dan “pendek” dari torus.

Sumber

$\peluru$ Kyle Celano, Vincent E. Coll & Jeff Dodd (2022): Mengapa Kurva Kurva: Geodesik di Torus, Majalah Matematika, 95:3, 230–239, DOI: 10.1080/0025570X.2022.2055349

$\peluru$ Jantzen, Robert T., 2021: Geodesik di Torus dan Permukaan Revolusi lainnya. ArXiv.

$\peluru$ William Schulz, Geometri Diferensial menyerang torus. PDF.

Leave a Comment Cancel reply