Hi, Selamat datang di wikitanic.com.
Ini adalah kiriman tamu oleh James Grime, superstar matematika serba bisa, dengan siapa tidak mungkin untuk bercakap-cakap tanpa seseorang meminta selfie atau tanda tangan. Dia tidak setuju dengan cerita saya tentang bencana Truchet dan saya senang membiarkan dia meluruskannya.
Jika Anda ingin melihat matematika dengan cara baru dan menarik, Anda harus mengunjungi MathsCity, pusat penemuan matematika baru di Leeds. Seperti pusat penemuan sains, ada banyak pameran fisik dan langsung, tetapi semuanya tentang matematika. Ada teka-teki untuk dipecahkan, dan permainan untuk dimainkan, dan Anda bisa berdiri di dalam gelembung raksasa! Anda juga akan menemukan satu set balok Truchet raksasa, yang dapat digunakan untuk membuat pola blobby yang menyenangkan.

Sangat menyenangkan untuk membuat pola blobby. Anda dapat mencoba menumpuknya menjadi kubus dan melihat apakah Anda dapat menghubungkan semua gumpalan. Dan jika Anda ingin serius tentang itu, Anda dapat berbicara tentang bahan seperti batu pasir, yang sangat mirip dengan pola Truchet, dan matematika di balik yang baru saja memenangkan medali Fields.
Atau, Anda bisa membuat pola blobby saja.
Sebenarnya, saya ditugaskan untuk mendesain set kubus Truchet ini untuk MathsCity. Jadi, tentu saja, pertanyaan saya adalah, ada berapa kubus Truchet? Setelah beberapa pekerjaan, saya yakin jawabannya adalah 16, jadi kami membuat satu set lengkap 16 kubus Truchet.
Namun, kebetulan Colin Beveridge ((Hei! Itu nama saya! – Ed)) sedang mempertimbangkan masalah yang sama dan sama yakinnya bahwa jawabannya adalah 10. Salah satu dari kami pasti salah. Satu ahli matematika akan menang dan yang lainnya diselimuti rasa malu.
Ternyata kami berdua salah.
Pendekatan saya telah menyebabkan saya menghitung terlalu banyak jumlah solusi, sementara pendekatan Colin menyebabkan dia menghitung jumlah solusi yang kurang. Hanya dengan membandingkan dua pendekatan kami, kami melihat kesalahan kami sendiri, dan akhirnya menetapkan angka yang benar.
Pendekatan saya terlalu rumit. Saya mulai dengan fakta bahwa setiap permukaan adalah ubin Truchet. Artinya, setiap sisi berbentuk persegi dengan seperempat lingkaran di pojok kiri atas dan pojok kanan bawah, atau petak yang sama tetapi diputar 90 derajat. Saya menyebut kedua ubin ini 0 dan 1.


Saya kemudian membayangkan sebuah kubus, diratakan menjadi jaring, dan mengisi keenam sisinya dengan ubin 0 atau ubin 1. Anda dapat menganggap keenam sisi ini sebagai bilangan biner enam digit dari 0 hingga 63. Tetapi beberapa kubus ini ekuivalen. Dengan kata lain, memutar kubus mungkin memberi kita salah satu solusi lain. Jadi saya membahas setiap kemungkinan, dan memikirkan tentang bagaimana 24 kemungkinan rotasi akan memengaruhi bilangan biner kubus. Ini menghasilkan delapan kubus yang tidak setara.

Akhirnya, yang harus saya lakukan hanyalah mewarnai kubus. Misalnya, saya bisa mewarnai kubus hitam dan putih. Atau saya mewarnai kubus yang sama dengan dua warna yang ditukar. Itu akan memberi saya dua kemungkinan pewarnaan untuk setiap kubus untuk membuat total 16 kubus.
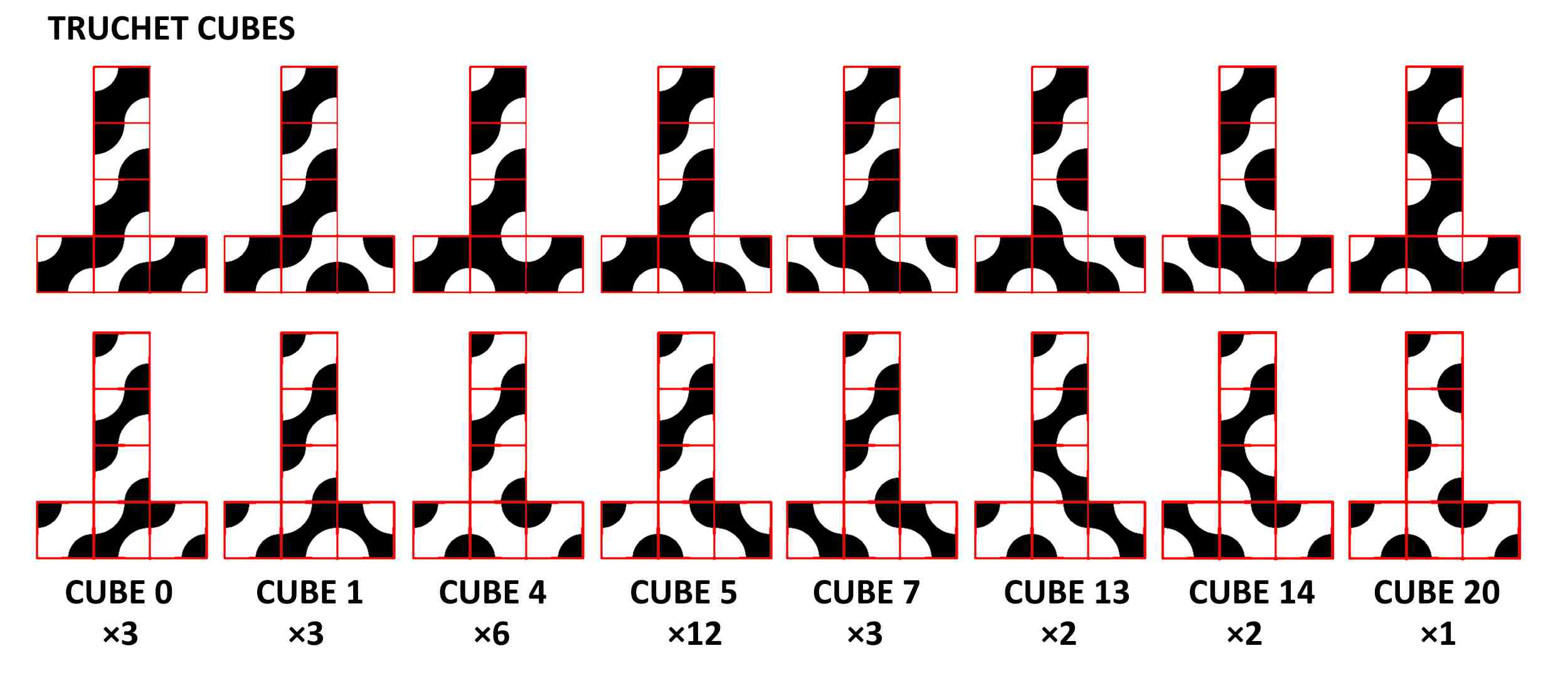
Pendekatan Colin untuk masalah yang sama jauh lebih sederhana. Colin mulai dengan ubin yang sudah diwarnai. Dalam hal ini, setiap permukaan dapat dianggap sebagai ubin dengan garis hitam, atau ubin dengan garis putih.


Sekarang pertanyaannya menjadi, seperti apa bentuk kubus dengan 0 garis hitam, 1 garis hitam, 2 garis hitam, dan seterusnya. Setelah berpikir sejenak, Colin menemukan sepuluh kemungkinan.
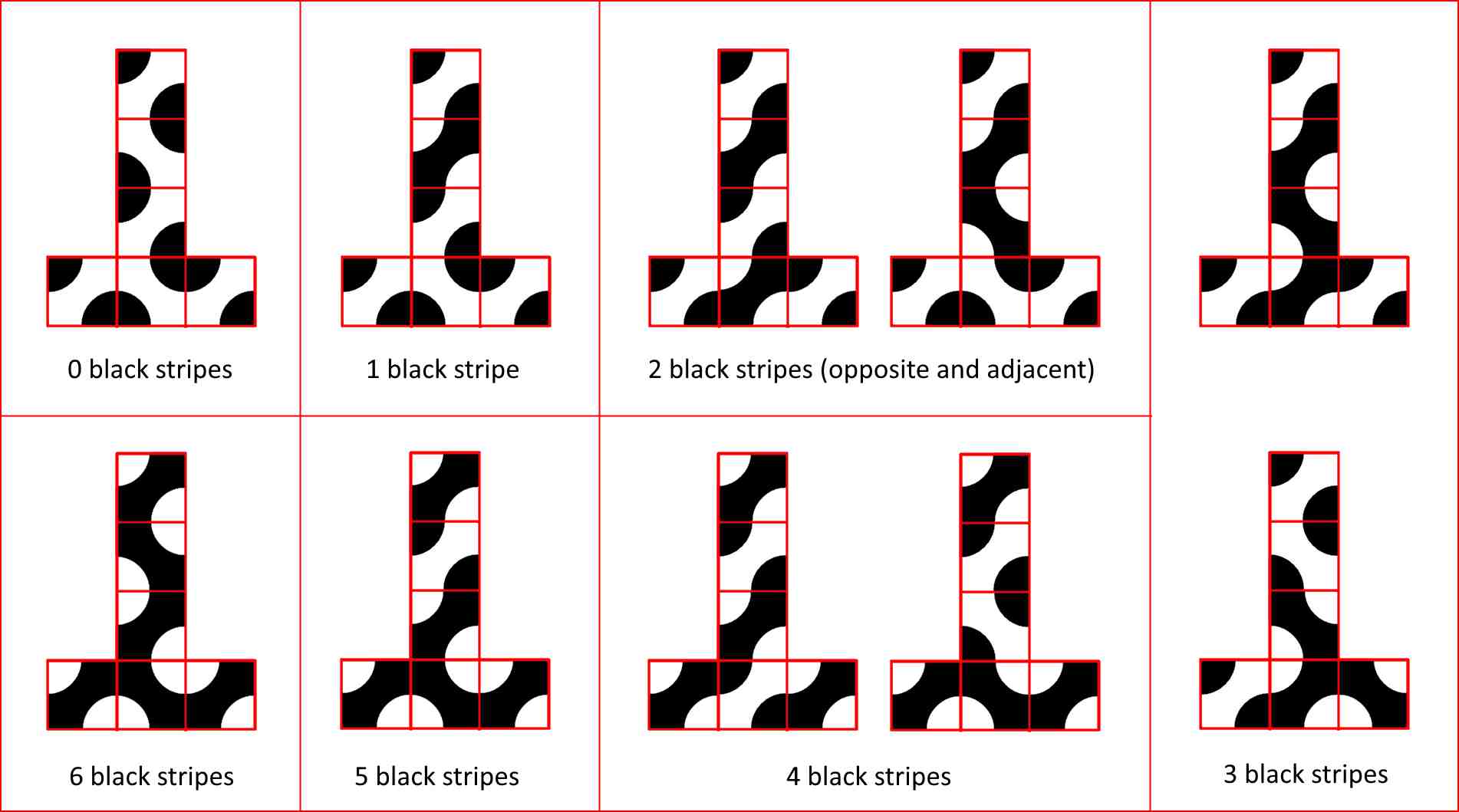
Ketika saya melihat solusi Colin, saya khawatir. Itu jauh lebih elegan dari saya, dan itu memiliki jawaban yang sama sekali berbeda. Saya kembali dan memeriksa solusi saya. Dan ya, ternyata saya telah menghitung terlalu banyak. Faktanya, semua kubus dengan tiga garis hitam adalah kebalikan diri – jika kita menukar dua warna kita mendapatkan kubus yang sama.
Tetapi jika itu benar, maka jumlah kubus Truchet yang tidak setara seharusnya 12, dan bukan 10 yang dimiliki Colin. Ternyata Colin juga melewatkan kehalusan dengan kubus dengan tiga garis juga. Tiga garis hitam dapat berbaris untuk membuat satu garis panjang, atau dapat bertemu di sudut. Tapi ada dua versi kubus dengan garis-garis panjang, dan dua cara tiga garis dapat bertemu di sudut (satu di mana mereka bertemu di sudut, dan satu di mana mereka membuat “lubang” di sudut).
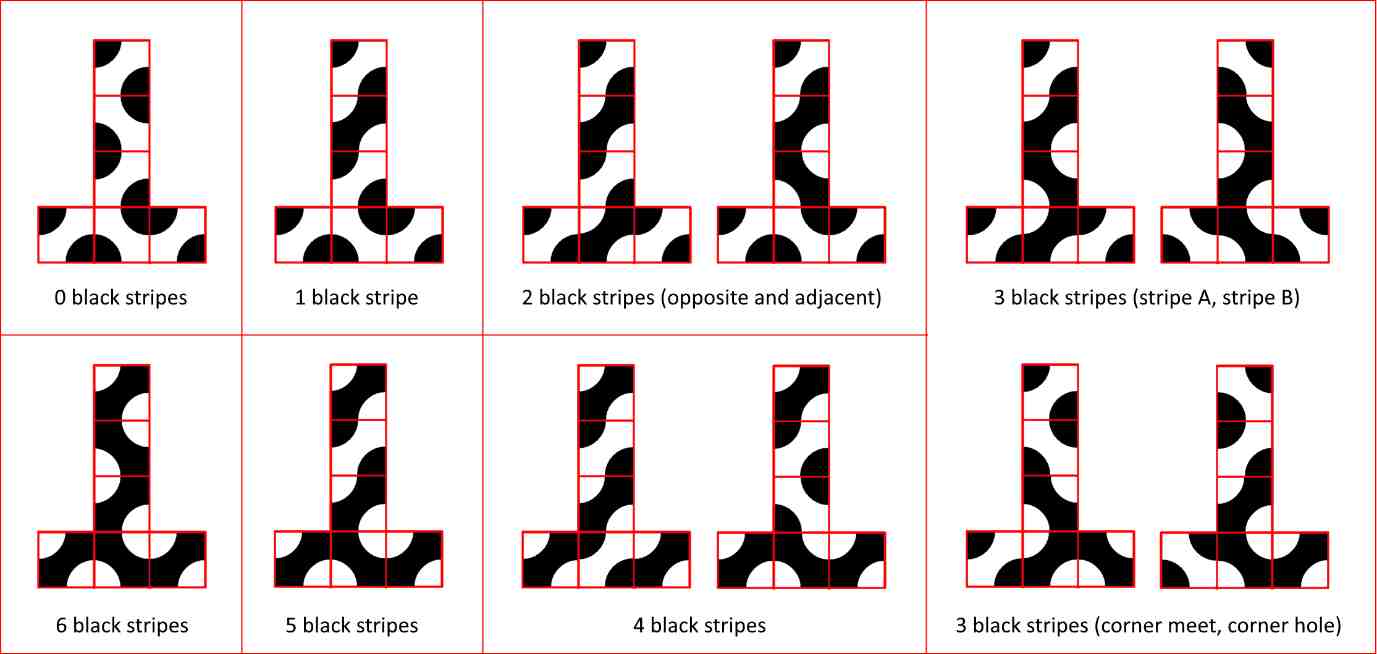
Ini ternyata menjadi teka-teki yang sangat bagus untuk dipecahkan. Ini tidak terlalu sulit, dengan ruang lingkup untuk menyelesaikannya dengan cara yang berbeda, tetapi dengan beberapa kehalusan yang menghentikannya menjadi sangat mudah. Itu pasti membodohi saya dan Colin, dan kami mungkin sangat jenius, jadi pasti sulit.
Yah, tidak juga. Ada kesalahan dalam kedua upaya kami. Tetapi dengan membandingkan solusi kami dan menggabungkan pendekatan kami, kami dapat membuat satu mega-jenius.
