Halo, Selamat datang di wikitanic.com.
Volume bola adalah berapa banyak ruang yang ditempati bola. Pada gambar di bawah, perhatikan bahwa bola di sebelah kiri menempati lebih sedikit ruang daripada bola di sebelah kanan. Oleh karena itu, bola di sebelah kiri memiliki volume yang lebih kecil.
Volume rumus bola
Mengingat jari-jari, volume dapat ditemukan dengan menggunakan rumus berikut:
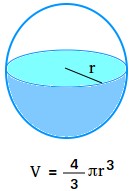
V = (4/3)pir3 = (4/3)πr3
pi atau π adalah konstanta matematika khusus, dan kira-kira sama dengan 22/7 atau 3,14.
Jika r atau jari-jari bola diketahui, volumenya adalah empat pertiga hasil kali pi dan pangkat tiga dari jari-jari bola.
Misalkan diameter diberikan, bukan jari-jari. Karena jari-jari adalah setengah dari diameter, bagilah diameter dengan 2 untuk mendapatkan jari-jari sebelum mencari volume.
Jika Anda harus menggunakan diameter, V = (4/3)π(d/2)3 = (4/3)Pi(d3/8) = 4pd3/24 = πd3/6
Volume dinyatakan dalam satuan kubik.
- Jika r diukur dalam meter, maka volume diukur dalam meter kubik atau m3.
- Jika r diukur dalam sentimeter, maka volume diukur dalam sentimeter kubik atau cm3.
- Jika r diukur dalam inci, maka volume diukur dalam inci kubik atau in.3
Beberapa contoh menunjukkan bagaimana mendapatkan volume bola
Contoh 1
Temukan volume bola yang memiliki jari-jari 2 inci
Volume = 4/3 × π × r3
Volume = 4/3 × 3,14 × 23
Volume = 4/3 × 3,14 × 8
Volum = 4/3 × 25,12
Volume = 4/3 × 25,12 / 1
Volume = (4 × 25,12)/(3 × 1)
Volume = (100,48) / 3
Volume = 33,49 inci kubik = 33,49 inci.3
Contoh #2
Temukan volume bola dengan jari-jari 3 kaki
Volume = 4/3 × π × r3
Volume = 4/3 × 3,14 × 33
Volume = 4/3 × 3,14 × 27
Volum = 4/3 × 84,78
Volume = 4/3 × 84,78/1
Volume = (4 × 84,78)/(3 × 1)
Volume = (339,12)/3
Volume = 113,04 kaki3 = 113,04 kaki kubik
Contoh #3
Hitung volume bola dengan jari-jari 2/3 cm
Volume = 4/3 × π × r3
Volume = 4/3 × 3,14 × (2/3)3
Volume = 4/3 × 3,14 × 2/3 × 2/3 × 2/3
Volume = 4/3 × 3,14 × 8/27
Volume = 4/3 × 3,14/1 × 8/27
Volume = (4 × 3,14 × 8) / ( 3 × 1 × 27 )
Volume = (100,48)/(81)
Volume = 1,24 inci.3
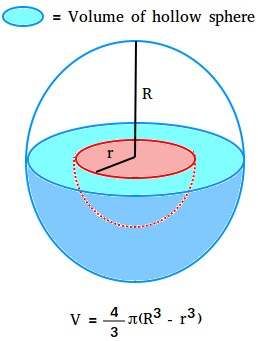
Volume bola berongga
Misalkan bola dengan jari-jari dalam r dipindahkan dari bola dengan jari-jari luar R. Apa yang Anda dapatkan disebut bola berongga atau bola yang memiliki rongga di dalamnya. Pada gambar di bawah, rongga ditunjukkan dengan warna merah.
Volume rongga adalah volume bola yang dikeluarkan.
Volume bola berongga adalah apa pun yang tersisa setelah volume rongga dihilangkan. Ini ditunjukkan dengan warna aquamarine.
Volume bola berongga = volume seluruh bola – volume rongga.
Volume bola berongga = (4/3) halR3 – (4/3) halr3
Faktor keluar (4/3) hal
Volume bola berongga = (4/3)π(R3 – r3)
Volume belahan bumi
Belahan adalah setengah bola. Untuk mencari volume setengah bola, cukup bagi rumus untuk mencari volume dengan 2.
V = [(4/3)πr3]/2
V = (2/3)πr3
Volume belahan adalah dua pertiga produk pi dan pangkat tiga jari-jari bola.
Volume bola menggunakan keliling bola
C = 2pr
V = (4/3)pr3
r = C/2π
V = (4/3)π(C/2π)3
V = (4/3)π(C3/8p3)
V = (4πC3)/(24 hal3)
V = (4pC3)/(4p)(6 hal2)
Membatalkan 4p
V = (C3)/(6p2)
Berapa volume bumi?
Bumi berbentuk bulat dengan radius 6356 kilometer atau 3958,8 mil. Berapa volume bumi dalam mil kubik?
Volume bumi = 4/3 × π × 3958,83
Volume bumi = 4/3 × 3,14 × 3958,8 ×3958,8 × 3958,8
Volume bumi = 4/3 × 3,14 × 62042699345,5
Volume bumi = 4/3 × 194814075945
Volume bumi = 4/3 × 194814075945/1
Volume bumi = (4 × 194814075945)/(3 × 1)
Volume bumi = (779256303779)/(3)
Volume bumi = 259.752.101.260 mil kubik
Bumi memiliki volume kira-kira 260 triliun mil kubik.
Penurunan volume bola
Kita membutuhkan kalkulus, khususnya konsep integrasi, untuk menurunkan volume bola atau untuk menunjukkan buktinya. Lihatlah bidang di bawah ini dan pelajari dengan cermat!
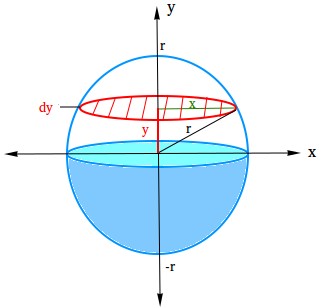
- Lingkaran merah adalah cakram tipis. Anggap saja sebagai silinder yang sangat datar!
- x adalah jari-jari cakram tipis
- dy adalah ketebalan piringan tipis
- r adalah jari-jari bola
- y adalah jarak dari sumbu x ke piringan.
Menggunakan teorema Pythagoras, r2 = x2 + y2
x2 = r2 – y2
Volume piringan tipis pada ketinggian tertentu adalah πx2dy
Pengganti r2 – y2 untuk x2 dalam πx2dy
V = π(r2 – y2)dy
Volume total bola ditemukan dengan menambahkan volume semua disk untuk semua ketinggian yang memungkinkan Anda dapat meletakkan disk tersebut di dalam bola.
Semua ketinggian yang mungkin adalah antara -r dan r (-r ≤ y ≤ r)
Tanda yang Anda lihat di bawah ini adalah simbol integral dan merupakan penjumlahan, artinya menjumlahkan semuanya.
$$ \int_^ $$
Yang di bawah berarti menambahkan semuanya dari -r ro r
$$ \int_-r^r $$
Yang di bawah berarti menjumlahkan volume semua disk untuk semua ketinggian yang memungkinkan, Anda dapat meletakkan disk tersebut (-r ≤ y ≤ r).
$$ \int_-r^r π(r^2 – y^2) \,dy $$
Menurut aturan linearitas, Anda dapat memindahkan pi di luar tanda integral.
$$ π \int_-r^r (r^2 – y^2) \,dy $$ $$ π \int_-r^r (r^2 – y^2) \ ,dy = π[yr^2 – \frac y^33 ]_-r^ r $$ $$ π \int_-r^r (r^2 – y^2) \,dy = π[(r^3 – \frac r^33 – (-r^3 – \frac -r^33 )]
$$ $$ π \int_-r^r (r^2 – y^2) \,dy = π[( \frac 2r^33 – ( \frac -2r^33 )]
$$ $$ π \int_-r^r (r^2 – y^2) \,dy = π[( \frac 2r^33 + ( \frac 2r^33 )]
$$ $$ π \int_-r^r (r^2 – y^2) \,dy = π( \frac 4r^33) $$ $$ π \int_- r^r (r^2 – y^2) \,dy = (\frac43πr^3) $$