Kalkulus Topologis: singkirkan epsilon dan delta yang buruk itu

Hello, Selamat datang di wikitanic.com.

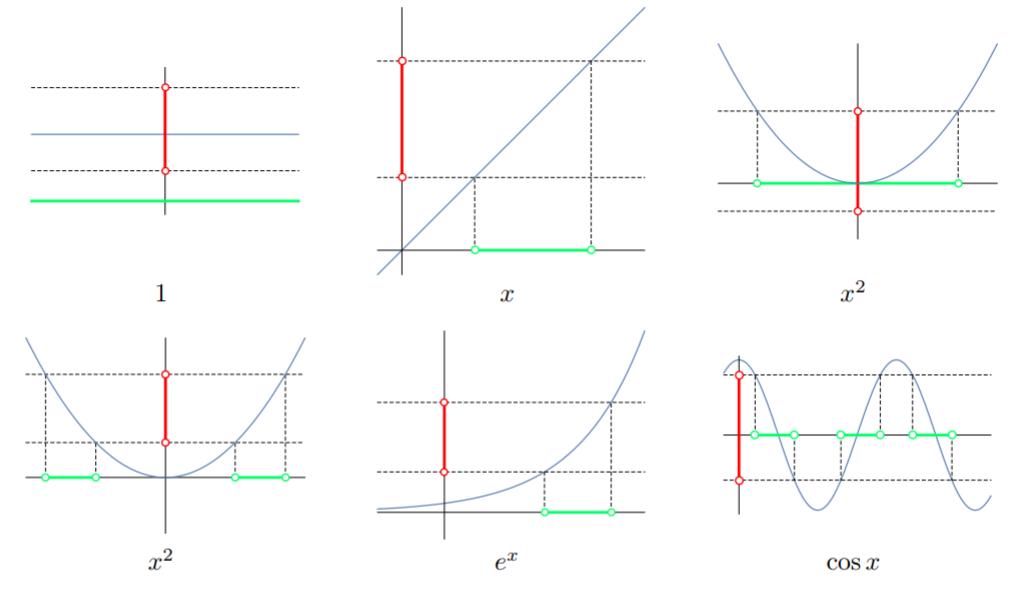
Fungsi terus menerus[figure from Olver (2022a).

A new approach to calculus has recently been developed by Peter Olver of the University of Minnesota. He calls it “Continuous Calculus” but indicates that the name “Topological Calculus” is also appropriate. He has provided an extensive set of notes, which are available online (Olver, 2022a)].

Motivasi

Siswa yang memulai program universitas dalam matematika sering merasa “dibombardir” oleh epsilon dan delta. Selama hampir 200 tahun, analisis matematis didasarkan pada formalisme yang diperkenalkan oleh Bolzano, Cauchy dan Weierstrass. Untuk mengatasi kesulitan yang terkait dengan jumlah yang sangat kecil, mereka mendefinisikan batas, kontinuitas, turunan, dan integral menggunakan $\varepsilon-\delta$ teknik.

Fungsi bernilai nyata $f(x)$ memiliki batas $SEBUAH$ pada $x_0$ jika, diberikan positif $\varepsilon$ betapapun kecilnya, bilangan positif $\delta>0″ class=”latex” /> dapat ditemukan sehingga, kapan pun <img decoding=$ kita punya ${|f(x)-A|<\varepsilon}$ . Jika itu semua Yunani untuk Anda, maka Anda tidak sendirian. Biarkan saya membuatnya lebih buruk: $SEBUAH$ adalah batas dari $f(x)$ pada $x=x_0$ dengan ketentuan

$\displaystyle \forall\varepsilon>0\ \exists\delta>0 : 0<|x-x_0|<\delta \implies |f(x)-A|<\varepsilon \,.$

Tidak sulit membayangkan kebingungan seorang siswa muda melihat ini untuk pertama kalinya.

Augustin-Louis Cauchy pada tahun 1821 dan, kemudian, Karl Weierstrass, memformalkan definisi limit suatu fungsi yang kemudian dikenal sebagai $(\varepsilon, \delta)$ definisi batas. Namun, pada tahun 1817, Bernard Bolzano telah memperkenalkan ide dasar teknik epsilon-delta, meskipun karyanya tidak diakui selama masa hidupnya.

Cara yang Lebih Baik

Titik awal bagi Olver adalah gagasan bahwa gerak terus menerus: jika sesuatu bergerak dari $SEBUAH$ ke $B$ , itu harus melewati jalur kontinu antara dua titik ini. Ini adalah ide yang dapat diakses dan jelas secara intuitif (kecuali jika Anda adalah Zeno!). Olver menyajikan argumen dalam sebuah artikel di Sang Kecerdasan Matematika (Over, 2022b).

Kontinuitas topologi didefinisikan sebagai berikut: Suatu fungsi kontinu jika dan hanya jika bayangan terbalik dari setiap himpunan terbuka adalah terbuka. Karakterisasi ini lebih umum, namun lebih sederhana, daripada definisi berbasis batas yang biasanya digunakan dalam kalkulus. Olver menyadari bahwa dia dapat mengembangkan kalkulus dasar menggunakan ide ini sebagai titik awal. Dia melihat bahwa dia bisa membangun definisi turunan, integral dan konvergensi dengan cara yang ketat sambil menghilangkan semua referensi ke epsilon dan delta. Dalam perkembangannya, kontinuitas adalah konsep dasar. Batas tidak penting tetapi diperkenalkan untuk kenyamanan (mendefinisikannya dalam hal kontinuitas). Definisi turunan dari suatu fungsi mengikuti secara langsung.

Olver mulai dengan fungsi bernilai nyata pada garis nyata. Sebuah topologi $\mathcalO$ pada $\mathbbR$ dibangun dari serikat interval terbuka. Definisi topologi kontinuitas dapat dengan mudah dimotivasi dengan mempertimbangkan gambar terbalik dari inerval terbuka. Siswa akan perlu belajar tentang sifat topologi dari garis nyata. Namun, mereka membutuhkan pengetahuan tersebut untuk kemajuan lebih lanjut dalam matematika, dan biasanya mempelajarinya secara paralel dengan analisis dasar.

Kontinuitas

Definisi kontinuitas topologi berasal dari Felix Hausdorff (1914):

Definisi. Sebuah fungsi $f : \mathbbR\rightarrow\mathbbR$ kontinu jika, kapanpun $S \subset \mathbbR$ terbuka, maka $f^-1(S) \subset\mathbbR$ terbuka.

Dari sini, Olver membuktikan sifat biasa dari fungsi kontinu: fungsi $f(x) \pm g(x)$ , $f(x)g(x)$ dan $f(x)/g(x)$ terus menerus ( $g(x)\ne 0$ dalam kasus terakhir). Dia kemudian membuktikan Teorema Nilai Menengah, Teorema Bolzano-Weierstrass, Teorema Nilai Ekstrim dan Teorema Heine-Borel.

Batas, yang tidak penting tetapi nyaman, didefinisikan sebagai berikut. Memperkirakan $f : I_a \rightarrow \mathbbR$ kontinu pada interval tertusuk $I_a : \mathbbR\setminus\a\$ . Kami mengatakan itu $f(x)$ memiliki nilai yang membatasi $z \di \mathbbR$ pada $x = a$ jika

$\displaystyle \hat f: I \rightarrow R \qquad\mboxgiven by\qquad \hat f(x) = \begincases f(x), &x \ne a \\ z, &x = a \end kasus$

terus menerus. Dalam hal ini, kami menulis $\lim_x\panah kanan a f(x) = z$ . Olver kemudian menunjukkan bahwa karakterisasi kontinuitas limit mencakup perilaku limit dari barisan bilangan real $\f_1, f_2, f_3, \dots \$ .

Diferensiasi

Sekarang definisi turunan dapat diberikan menggunakan kontinuitas:

Definisi. Membiarkan $f: \mathbbR \rightarrow \mathbbR$ terus menerus. Kemudian $f(x)$ memiliki turunan di $a \di \mathbbR$ jika ada $z \di \mathbbR$ sehingga fungsi hasil bagi perbedaan

$\displaystyle q(x) = \begincases \displaystyle\fracf(x)-f(a)xa, &x \ne a \\ z, &x = a \endcases$

terus menerus. Dalam hal ini, kami menulis $f^\prima(a) = z$ atau, setara,

$\displaystyle f^\prime(a) = \lim_x\rightarrow a \fracf(x)-f(a)xa \,.$

Olver menunjukkan bahwa ide ini berasal dari matematikawan Yunani Constantin Carathéodory pada awal abad kedua puluh. Dia kemudian menurunkan semua rumus biasa kalkulus dasar: turunan dari jumlah, produk dan hasil bagi dari fungsi yang dapat dibedakan, dan bentuk eksplisit untuk turunan dari beberapa fungsi aljabar dan trigonometri. Teorema Rolle dan Teorema Nilai Rata-rata kemudian dibuktikan. Turunan orde tinggi dan teorema Taylor mudah ditangani dalam formalisme pendekatan ini.

Olver sekarang beralih ke topologi bidang, dan membahas fungsi kontinu, konvergensi seragam, dan turunan parsial dalam konteks ini. Dia menyimpulkan dengan beberapa bab tentang integrasi, tiba di Teorema Dasar Kalkulus.

Kesimpulan

Pendekatan kontinuitas kalkulus menarik dari perspektif pedagogis: menyederhanakan bukti dari banyak teorema penting, khususnya yang melibatkan diferensiasi. Seperti yang Olver amati, “gangguan dan komplikasi epsilon dan delta benar-benar hilang tanpa pengorbanan apa pun secara kaku atau umum!”

Siswa perlu meluangkan waktu untuk mempelajari topologi garis dan bidang yang sebenarnya, tetapi ini mendasar, dan layak dipelajari. Olver menyimpulkan bahwa judul yang lebih akurat dari pendekatannya adalah “Kalkulus Topologi”, karena pada dasarnya topologi dan independen dari pilihan metrik. Akan menarik untuk mempelajari bagaimana pendekatan ini bekerja dalam konteks dunia nyata dari sebuah ruang kelas.

Sumber

$\peluru$ Hausdorff, Felix, 1914: Dasar-dasar teori himpunan, Verlag Veit & Co, Leipzig. 476 hal.

$\peluru$ Olver, Peter J., 2022a: Kalkulus Berkelanjutan. Catatan Kuliah, Univ. Minnesota, 131 hal. PDF.

$\peluru$ Olver, Peter J., 2022b: Gerak dan kontinuitas, Matematika. Intelijen, 44, 241–249. Pracetak PDF.

$\star \qquad \star \qquad \star$

Kursus UCD tentang matematika rekreasi, AweSums: Keajaiban, Kegunaan, dan Kegembiraan Matematikaakan dipresentasikan pada musim gugur ini oleh Prof Peter Lynch — masih ada beberapa tempat, dan pendaftaran dibuka di www.ucd.ie/lifelonglearning

$\star \qquad \star \qquad \star$

MALAM INI

Kuliah Berkeley 2022, Universitas Maynooth

“Tingkat Tak Terbatas”

Pembicara: Peter Lynch

Teater Kuliah John Hume 4, Kampus Utara

$\star \qquad \star \qquad \star$

Leave a Comment Cancel reply