Halo, Selamat datang di wikitanic.com.

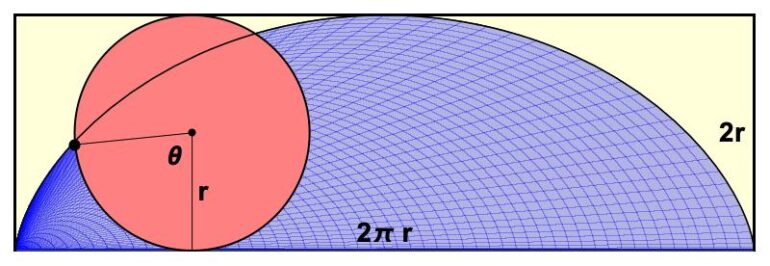
Cycloid, tempat kedudukan suatu titik di tepi piringan yang berputar.
Banyak penulis menggunakan metafora matematika dengan efek yang besar. Sebuah buku terbaru, “Sekali Perdana” oleh Sarah Hart, menggambarkan hubungan menakjubkan antara matematika dan sastra. Sebagai contoh khusus, dia membahas relevansi kurva sikloid dalam karya Herman Melville. Buku Moby-Dickpertama kali diterbitkan pada tahun 1851, dibuka dengan kata-kata “Panggil aku Ismael”, dan diakhiri dengan Ismael sebagai satu-satunya yang selamat dari pelayaran tersebut.
Moby-Dick
Di dalam Moby-DickMelville menggunakan banyak gambar matematika, dan dia menggunakan sifat kurva matematika yang disebut sikloid — kurva yang dilacak oleh titik di tepi roda yang berputar — untuk menjelaskan pengamatan Ismael terhadap gerakan batu sabun dalam kuali besar.
Melville memiliki pendidikan yang terbatas, tetapi dia beruntung bisa bersekolah di Akademi Albany, di mana dia menjadi murid Joseph Henry, seorang ilmuwan terkenal, yang kemudian menjadi Sekretaris pertama Institusi Smithsonian (SI unit induktansi dinamai Henry). Ajaran Henry memiliki dampak mendalam dan bertahan lama pada Melville, yang mempertahankan ketertarikannya pada matematika (Bellini, 2022).
Bellini (2022) menjelaskan sebuah insiden di Bab XCVI dari Moby-Dick, di mana Ismael sedang membersihkan “periuk”, sebuah kuali besar tempat lemak direbus untuk membuat minyak ikan paus. Panci ini dijaga kebersihannya dengan menggosoknya dengan batu sabun yang berat. Saat Ismael berdiri di dalam kuali, menggosok, dia terpukul
“… fakta yang luar biasa, bahwa dalam geometri semua benda meluncur di sepanjang sikloid, wah
soapstone misalnya, akan turun dari titik mana pun pada waktu yang bersamaan.”
Di sini Ismael merujuk pada sifat sikloid yang menarik, kurva yang dihasilkan oleh titik di tepi roda bundar yang menggelinding. Ismael memperhatikan sifat “waktu yang sama” dari permukaan bagian dalam dan, bahkan dengan pengetahuannya yang terbatas, tampaknya menyimpulkan bahwa try-pot harus memiliki penampang dalam bentuk sikloid.
Cycloid memainkan peran penting dalam pengembangan kalkulus dan dipelajari secara intensif oleh beberapa ahli matematika terkemuka di abad ketujuh belas. Christiaan Huygens menemukan bahwa, jika sebuah titik massa ditempatkan di mana saja pada kurva sikloid dan bergerak tanpa gesekan, ia mencapai titik terendah “tepat pada waktu yang sama”, seperti yang diamati oleh Ismael. Untuk alasan ini, Huygens menyebut kurva itu tautokron (arti sama waktu), dan dia menggunakannya dalam desain jam pendulum yang akurat.

Partikel mulai dari diam di titik P dan di Q mencapai dasar, titik O, tepat pada waktu yang bersamaan.
Brachistochrone
Cycloid memiliki properti luar biasa lainnya, yang memberinya nama lain. Johann Bernoulli-lah yang menemukan bahwa sebuah partikel yang bergerak di bawah gravitasi antara dua titik A dan B dalam bidang vertikal membutuhkan waktu paling sedikit jika lintasannya berbentuk sikloid. Properti ini membuat Bernoulli menamai cycloid sebagai brachistochrone (dari bahasa Yunani Brachisterpendek, dan Kronoswaktu).
Setelah memecahkan masalah ini, Bernoulli mengeluarkannya sebagai tantangan bagi ahli matematika Eropa lainnya. Salah satu solusi paling penting, yang konon ditemukan dalam satu malam, adalah solusi dari Isaac Newton. Inilah cara Bernoulli mengumumkan tantangannya:
Masalah Mekanik-Geometris pada Kurva Keturunan Tercepat.
‘Untuk menentukan kurva jointing dua titik tertentu, pada jarak yang berbeda dari horizontal dan
tidak pada garis vertikal yang sama dengan partikel bergerak, yang dipengaruhi oleh beratnya sendiri dan
memulai gerakannya dari titik atas, turun paling cepat ke titik bawah.’
Bernoulli senang menemukan bahwa masalah brachistochronenya melibatkan kurva yang sama, sikloid, seperti masalah tautochrone Huygens. Seperti dikutip oleh Kimball (1955):
“Kamu akan membatu dengan keheranan ketika aku mengatakan itu dengan tepat
cycloid ini, tautochrone dari Huygens, adalah brachistochrone kami …
Selain itu, saya pikir ini patut dicatat identitas ditemukan
hanya di bawah hipotesis Galileo, sehingga bahkan dari ini
kita dapat menduga bahwa alam menginginkannya demikian.
Untuk penjelasan lengkap dan menarik tentang masalah brachistochrone, lihat Kimball (1955).
Sumber
- Federico Bellini, 2022: “Kurva Melville: Matematika dan Imajinasi Melville. Mengukur Cycloid di Moby-Dick”, Miranda [Online], 26 | 2022. URL. DUA.
- Kimball, William S., 1955: Sejarah Brachistochrone. Pi Dalam Jurnal Epsilon, 2, No.2, hlm.57-77. JSTOR.
- Sarah Hart, 2003: Sekali Perdana. Mudlark, x+290pp. ISBN: 978-0-0086-0108-9.