Hey, Selamat datang di wikitanic.com.
Probabilitas bersyarat berisi kondisi yang memaksa Anda memusatkan perhatian pada subhimpunan ruang sampel. Misalnya, sebuah perusahaan mungkin memiliki pria dan wanita yang bekerja untuk perusahaan tersebut. Namun, Anda mungkin ingin menjawab pertanyaan tentang laki-laki saja atau perempuan saja. Jika Anda berurusan dengan asuransi, Anda mungkin ingin menjawab pertanyaan tentang perokok saja atau bukan perokok saja.
Cara yang baik untuk memulai probabilitas bersyarat adalah dengan menggunakan tabel kontingensi.
Probabilitas bersyarat menggunakan tabel kontingensi
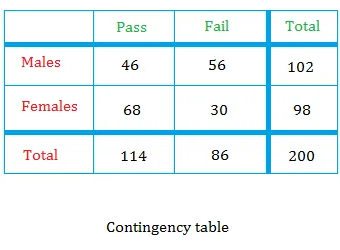
Berikut adalah cara mencari probabilitas bersyarat menggunakan tabel kontingensi yang kita gunakan dalam pelajaran tentang probabilitas marjinal. Tabel menunjukkan hasil tes untuk 200 siswa yang mengikuti tes GED.
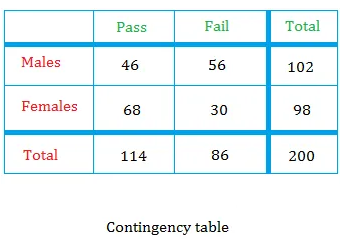
Dari daftar 200 siswa, kami memilih satu siswa secara acak. Namun, misalkan Anda sudah mengetahui siswa yang dipilih adalah laki-laki.
Fakta bahwa Anda mengetahui siswa tersebut adalah laki-laki berarti bahwa peristiwa tersebut telah terjadi. Dan itu memaksa Anda untuk memusatkan perhatian Anda hanya pada laki-laki atau 102 kemungkinan hasil.
Apa itu probabilitas bersyarat?
Mengetahui bahwa mahasiswa adalah laki-lakiAnda dapat menghitung kemungkinan yang dimiliki siswa ini lulus atau gagal. Probabilitas semacam ini disebut probabilitas bersyarat
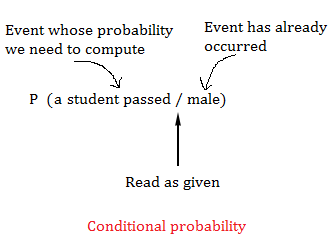
Notasi untuk mencari peluang bahwa ‘seorang siswa lulus jika siswa tersebut laki-laki adalah
P(mahasiswa lulus / laki-laki)
Anda sebenarnya bisa menghitung salah satu dari 8 probabilitas bersyarat berikut:
- P(mahasiswa lulus / laki-laki)
- P(mahasiswa lulus/perempuan)
- P(siswa gagal / laki-laki)
- P(siswa gagal/perempuan)
- P(siswa laki-laki/lulus)
- P(siswa laki-laki/gagal)
- P(mahasiswa perempuan/lulus)
- P(siswa perempuan/gagal)
Beberapa contoh menunjukkan bagaimana menemukan probabilitas bersyarat menggunakan tabel kontingensi
Contoh 1
Mari kita hitung P(seorang siswa telah lulus / laki-laki).
Jika siswa laki-laki, maka siswa tersebut akan diambil dari daftar 102 laki-laki.
Dari daftar ini hanya 46 siswa yang lulus.

P(mahasiswa lulus / laki-laki) =
Jumlah laki-laki yang lulus
Jumlah laki-laki
P(mahasiswa lulus / laki-laki) =
46
102
= 0,451
Contoh #2
Bagaimana dengan P(siswa laki-laki/lulus) ?
Jumlah siswa yang lulus sama dengan 114.
Dari daftar tersebut, hanya 46 siswa laki-laki.
P(siswa laki-laki/lulus) =
mahasiswa adalah laki-laki
Jumlah siswa yang lulus
P(siswa laki-laki/lulus) =
46
104
= 0,403
Seperti yang Anda lihat dari hasil P(mahasiswa lulus / laki-laki) tidak sama dengan
P(siswa laki-laki/lulus) karena ada perbedaan.
P(mahasiswa lulus / laki-laki): Probabilitas ini hanya menunjukkan tingkat keberhasilan pejantan saja.
P(siswa laki-laki/lulus): Probabilitas ini membandingkan tingkat keberhasilan laki-laki dengan perempuan.
Rumus probabilitas bersyarat
Perhatikan kembali rasio berikut:
P(mahasiswa lulus / laki-laki) =
Jumlah laki-laki yang lulus
Jumlah laki-laki
Biarkan M menjadi acara ‘siswa adalah laki-laki’
Misalkan P adalah kejadian ‘mahasiswa lulus’
Misalkan P∩M adalah kejadian ‘siswa laki-laki dan telah lulus’
n(P∩M) = jumlah siswa laki-laki yang lulus = 46
n(M) = jumlah siswa laki-laki = 102
P(P/M) =
n(P ∩ M)
n(M)
P(P/M) =
46
102
= 0,451
Kita bisa mendapatkan jawaban yang sama menggunakan probabilitas alih-alih menghitung. Bagilah pembilang dan penyebut dari rasio tepat di atas dengan 200.
P(P/M) =
46/200
102/200
P(P/M) =
0,23
0,51
= 0,451
P(P∩M) = probabilitas seorang siswa lulus jika siswa laki-laki = 46 / 200 = 0,23
P(M) = probabilitas seorang siswa laki-laki = 102 / 200 = 0,51
P(P/M) =
P(P ∩ M)
PM)
Kita kemudian dapat menyimpulkan bahwa ada dua cara untuk menemukan probabilitas bersyarat.
Cara menemukan probabilitas bersyarat dengan menghitung
Jika Anda berhadapan dengan kemungkinan hasil yang sama seperti melempar koin atau dadu adil dengan enam sisi, maka untuk dua kejadian A dan B, Anda dapat menggunakan rumus berikut:
P(A / B) =
n(A ∩ B)
n(B)
Cara mencari probabilitas bersyarat dengan menggunakan definisi probabilitas bersyarat
Apakah Anda berurusan dengan kemungkinan hasil yang sama atau tidak, maka untuk dua kejadian A dan B, Anda dapat menggunakan rumus berikut:
P(A / B) =
P(A ∩ B)
P(B)
Probabilitas A diberikan B adalah rasio probabilitas persimpangan A dan B terhadap probabilitas B.
Lebih banyak contoh probabilitas bersyarat
Contoh #3
Sebuah kartu diambil secara acak dari dek standar. Kartu tidak diganti. Tentukan peluang bahwa kartu kedua adalah raja jika kartu pertama yang ditarik adalah raja.
Misalkan K1 kejadian ‘keluarnya kartu pertama adalah raja’ dan K2 kejadian ‘keluarnya kartu kedua adalah raja’
Jika seorang raja ditarik dan tidak diganti, maka ada 3 raja yang tersisa dan dek sekarang akan memiliki 51 kartu.
P(K2 / K1) = 3/51 ≈ 0,0588
Dua kejadian A dan B disebut kejadian saling bebas jika P(A / B) = P(A)
Contoh #4
Misalkan H1 kejadian pelemparan koin pertama adalah kepala dan H2 adalah kejadian pelemparan kedua koin adalah kepala. Tunjukkan bahwa H1 dan H2 adalah kejadian yang saling bebas.
Perhitungan Anda harus menunjukkan bahwa P(H2 / H1) = P(H2)
Ruang sampel lengkapnya adalah HH, HT, TH, TT
H2 = HH, TH dan P(H2) = 0,50
Mengingat lemparan pertama adalah kepala, kita berakhir dengan HH, HT dan kita dibatasi pada dua hasil ini untuk menghitung P(H2 / H1)
Dari dua hasil ini, kita melihat bahwa HH (setengah dari 2 hasil) memiliki kepala sebagai lemparan kedua.
P(H2 / H1) = 0,5
P(H2 / H1) = P(H2) = 0,5, sehingga H1 dan H2 adalah kejadian yang saling bebas.
Dalam peristiwa yang berdiri sendiri, terjadinya suatu peristiwa tidak mempengaruhi terjadinya peristiwa lain. Di dalam contoh #4kejadian ‘Anda mendapatkan kepala dengan lemparan pertama atau H1’ tidak akan mempengaruhi kemungkinan mendapatkan kembali kepala dengan lemparan kedua.
Ini tidak terjadi dengan contoh #3 dimana terjadinya suatu peristiwa dapat mempengaruhi terjadinya peristiwa yang lain.
Dua kejadian A dan B disebut kejadian dependen jika P(A / B) ≠ P(A)
Di dalam contoh #3, P(K2 / K1) = 3/51. Namun, P(K2) = 4/52 = 0,076
Karena kartu pertama tidak diganti atau dimasukkan kembali ke tumpukan, kemungkinan undian kedua jelas tergantung pada hasil yang pertama,