Apa itu persamaan eksponensial?
Ini adalah persamaan yang eksponen atau bagian dari eksponennya adalah variabel.
Contoh:
3x = 27
53x – 1 = 625
Memecahkan Persamaan Eksponensial dengan Menulis Ulang Basis
Langkah-langkah berikut akan berguna untuk menyelesaikan persamaan eksponensial dengan menulis ulang basis.
Langkah 1 :
Dengan menggunakan aturan eksponen, tulis ulang setiap ruas persamaan sebagai pangkat dengan basis yang sama.
Langkah 2 :
Setelah Anda mendapatkan basis yang sama di kedua sisi pada langkah 1, samakan eksponen dan selesaikan variabelnya.
sebuahx =k
x = k
Contoh 1 :
Selesaikan untuk x :
3x = 27
Solusi:
3x = 27
3x = 3 3 3
3x = 33
Samakan eksponennya.
x = 3
Contoh 2 :
Selesaikan untuk x :
2x – 5 = 1/16
Solusi:
2x – 5 = 1/16
2x – 5 = 1/24
2x – 5 = 2-4
Samakan eksponennya.
x – 5 = -4
Tambahkan 5 di kedua sisi.
x = 1
Contoh 3 :
Selesaikan untuk x :
6 3x = 54
Solusi:
7 3x = 63
Bagilah kedua sisi dengan 7.
3x = 9
3x = 32
Samakan eksponennya.
x = 2
Contoh 4 :
Selesaikan untuk x :
4x = 7(2x) + 18
Solusi:
4x = 7(2x) + 18
(22)x = 7(2x) + 18
(2x)2 = 7(2x) + 18
(2x)2 – 7(2x) – 18 = 0
Misalkan a = 2x.
sebuah2 – 7a – 18 = 0
(a – 9)(a + 2) = 0
a – 9 = 0 atau a + 2 = 0
|
a – 9 = 0 a = 9 sebuah = 32 3x = 32 x = 2 |
a + 2 = 0 a = -2 a = -2 3x = -2 |
Dalam 3xberapapun nilai riilnya (positif atau negatif atau nol) kita substitusikan ke x, 3x tidak pernah bisa negatif. Jadi kita bisa mengabaikan persamaan 3x = -2.
Karena itu,
x = 2
Contoh 5:
Selesaikan untuk x :
5x = (√25)-7 (5)-5)
Solusi:
5x = (√25)-7 (5)-5
5x = 5-7 (51/2)-5
5x = 5-7 5-5/2
5x = 5-7 – 5/2
5x = 5-19/2
Samakan eksponennya.
x = -19/2
Menyelesaikan Persamaan Eksponensial Menggunakan Logaritma
Perhatikan persamaan berikut dalam bentuk eksponensial.
bkamu =
Gambar di bawah ini mengilustrasikan cara mengubah persamaan di atas dari eksponensial ke bentuk logaritma.
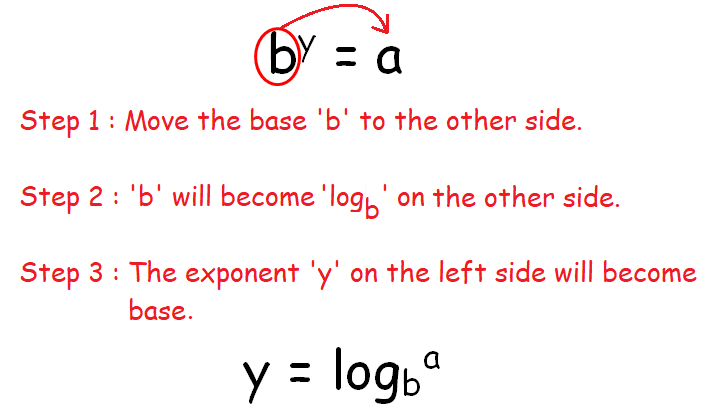
Masih kurang paham dengan apa yang dijelaskan di atas, silahkan tonton video di bawah ini untuk penjelasan langsung step by stepnya.
Contoh 6:
Tentukan nilai x jika 10x = 100.
Solusi:
10x = 100
Persamaan di atas dalam bentuk eksponensial. Ubah ke bentuk logaritmik untuk menyelesaikan x.
x = log10100
x = log10100
x = log10(102)
x = 2log1010
x = 2(1)
x = 2
Contoh 7 :
Tentukan nilai x jika 3x = 1/27.
Solusi:
3x = 1/27
Persamaan di atas dalam bentuk eksponensial. Ubah ke bentuk logaritmik untuk menyelesaikan x.
x = log3(1/27)
x = log31 – log327
x = 0 – log3(33)
x = -3log33
x = -3(1)
x = -3
Contoh 8 :
Tentukan nilai x jika 53x – 1 = 1/625.
Solusi:
53x – 1 = 1/625
Persamaan di atas dalam bentuk eksponensial. Ubah ke bentuk logaritmik untuk menyelesaikan x.
3x – 1 = log5(1/625)
3x – 1 = log51 – log5625
3x – 1 = 0 – log5(54)
3x – 1 = -4log55
3x – 1 = -4(1)
3x – 1 = -4
Tambahkan 1 ke kedua sisi.
3x = -3
Bagilah kedua sisi dengan 3.
x = -1
Menyelesaikan Persamaan Eksponensial dengan Basis Berbeda
Ketika kita menyelesaikan persamaan eksponensial, kita akan menggunakan aturan eksponen dan menulis ulang setiap sisi persamaan sebagai pangkat dengan basis yang sama.
Jika Anda tidak dapat menulis ulang setiap sisi persamaan sebagai pangkat dengan basis yang sama, ambil logaritma di kedua sisi persamaan dan selesaikan untuk x.
Contoh 9 :
Selesaikan untuk x :
2x – 1 = 5
Solusi:
2x – 1 = 5
Tambahkan 1 ke kedua sisi.
2x = 5
Di ruas kiri persamaan di atas, alasnya adalah 2. Di ruas kanan, 6 bukan pangkat 2. Jadi, kita tidak bisa mendapatkan bilangan yang sama di kedua ruas.
Ambil logaritma di kedua sisi dan selesaikan untuk x.
log(2x) = log6
Dengan menggunakan aturan pangkat logaritma,
xlog2 = log6
Bagilah kedua sisi dengan log2.
Contoh 10 :
Selesaikan untuk x :
5x – 1 – 2x = 0
Solusi:
5x – 1 – 2x = 0
Tambahkan 2x ke kedua sisi.
5x – 1 = 2x
Pada persamaan di atas, alas pada ruas kanan dan alas ruas kiri tidak sama. Dan juga, kita tidak bisa membuat basis yang sama di kedua sisi menggunakan aturan eksponen.
Ambil logaritma di kedua sisi dan selesaikan untuk x.
log(5x – 1) = log(2x)
Dengan menggunakan aturan pangkat logaritma,
(x – 1)log5 = xlog2
Dengan menggunakan sifat distributif,
xlog5 – log5 = xlog2
Kurangi xlog2 dari kedua sisi.
xlog5 – log5 – xlog2 = 0
Tambahkan log5 ke kedua sisi.
xlog5 – xlog2 = log5
Faktor.
x(log5 – log)2 = log5
Bagilah kedua sisi dengan (log5 – log2).
Kami selalu menghargai umpan balik Anda.