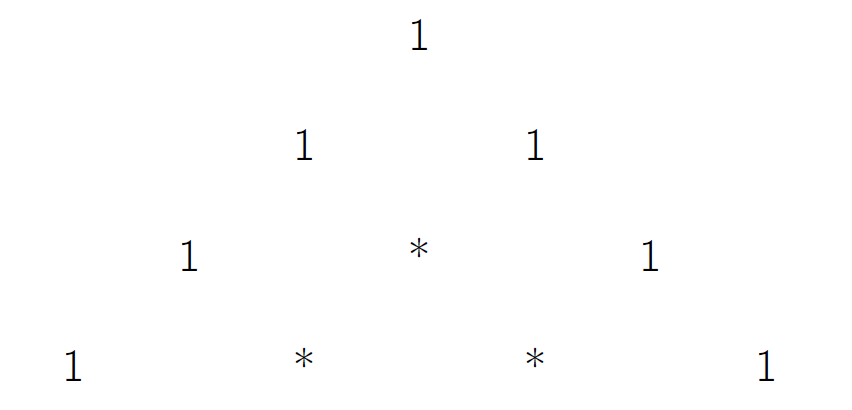Hey, Selamat datang di wikitanic.com.
Ekspresi binomial adalah jumlah, atau perbedaan, dari dua istilah.
Sebagai contoh,
x + 2, 2x + 3y, p – q
Kita mungkin sudah terbiasa dengan kebutuhan untuk memperluas tanda kurung saat mengkuadratkan jumlah tersebut.
Kita akan tahu, misalnya, bahwa
(x + 3)2 = (x + 3)(x + 3)
(x + 3)2 = x2 + 3x + 3x + 9
(x + 3)2 = x2 + 6x + 9
Jika kita ingin menaikkan ekspresi binomial ke pangkat lebih tinggi dari 2.
Misalnya jika kita ingin temukan (x + 3)7sayat agak sulit untuk melakukan ini dengan mengalikan berulang kali (x + 3) dengan dirinya sendiri.
Pada bagian ini, kita akan mempelajari bagaimana pola bilangan segitiga, yang dikenal sebagai segitiga Pascal, dapat digunakan untuk mendapatkan hasil yang diinginkan dengan sangat cepat.
segitiga pascal
Kita dapat membentuk segitiga Pascal menggunakan langkah-langkah yang dijelaskan di bawah ini.
Langkah 1 :
Kita mulai membuat segitiga Pascal dengan menuliskan angka 1.
Kemudian kita menulis baris baru dengan angka 1 sebanyak dua kali :
Langkah 2 :
Kami kemudian menghasilkan baris baru untuk membangun segitiga angka. Setiap baris baru harus dimulai dan diakhiri dengan 1 :
Langkah 3:
Angka yang tersisa di setiap baris dihitung dengan menjumlahkan dua angka pada baris di atas yang terletak di atas kiri dan kanan atas.
Jadi, menambahkan dua 1 di baris kedua menghasilkan 2, dan angka ini masuk ke ruang kosong di baris ketiga:
Langkah 4:
Dua ruang kosong pada baris keempat masing-masing ditemukan dengan menjumlahkan kedua bilangan pada
baris ketiga yang terletak di atas-kiri dan kanan-atas :
1 + 2 = 3 dan 2 + 1 = 3
Ini memberikan:

Langkah 5:
Kita dapat terus membangun segitiga dengan cara ini untuk menuliskan baris sebanyak yang kita inginkan.
Diagram di bawah menunjukkan enam baris pertama segitiga Pascal.

Segitiga Pascal dan Eksponen Binomial

Untuk memahami ekspansi aljabar segitiga pascal, mari kita perhatikan ekspansi (a + b)4 menggunakan segitiga pascal yang diberikan di atas.
Cara Mendapatkan Perluasan (a + b) Menggunakan Segitiga Pascal
Dalam (a + b)4eksponennya adalah ‘4’.
Jadi, mari kita ambil baris pada segitiga pascal di atas yang sesuai dengan 4th kekuasaan.
Itu adalah,
1 4 6 4 1
Peraturan umum :
Dalam ekspansi pascal, kita harus memiliki hanya ‘a’ di suku pertama, hanya ‘b’ di suku terakhir dan ‘ab’ di semua suku tengah lainnya.
Jika kita mencoba untuk mendapatkan ekspansi (a + b)nsemua istilah dalam ekspansi akan positif.
Catatan :
Aturan ini tidak hanya berlaku untuk kekuatan ‘4’.
Aturan ini berlaku untuk setiap nilai ‘n’ di (a + b).
Sudah dijelaskan dengan jelas di bawah ini.

Sekarang kita harus mengikuti langkah-langkah yang diberikan di bawah ini.
Langkah 1 :
Pada suku pertama, kita hanya perlu mengambil ‘a’ dengan pangkat ‘4’ [This is the exponent of (a + b)].
Maka suku pertamanya adalah a4.
Langkah 2 :
Pada suku kedua, kita harus mengambil ‘a’ dan ‘b’.
Untuk ‘a’, kita harus mengambil eksponen ‘1’ lebih kecil dari eksponen ‘a’ pada suku sebelumnya.
Untuk ‘b’, kita harus mengambil eksponen ‘1’.
Maka suku kedua adalah3b.
Langkah 3:
Di suku ketiga juga, kita harus mengambil ‘a’ dan ‘b’.
Untuk ‘a’, kita harus mengambil eksponen ‘1’ lebih kecil dari eksponen ‘a’ pada suku sebelumnya.
Untuk ‘b’, kita harus mengambil eksponen ‘2’.
Maka suku kedua adalah2b2.
(Kita harus melanjutkan proses ini, sampai kita mendapatkan eksponen ‘0’ untuk ‘a’)
Langkah 4:
Ketika kita melanjutkan proses yang disebutkan pada langkah 3, suku di mana kita mendapatkan eksponen ‘0’ untuk ‘a’ akan menjadi suku terakhir.
Dalam istilah terakhir, kita hanya akan memiliki ‘b’ dengan kekuatan ‘4’ [This is the exponent of (a + b)].
Maka suku terakhirnya adalah b4.
Empat langkah yang dijelaskan di atas diberikan pada gambar di bawah ini.

Akhirnya ekspansi adalah,
(a + b)4 =4 + 4a3b + 6a2b2 + 4ab3 + b4
Cara Mendapatkan Perluasan (a – b)Menggunakan Segitiga Pascal
Peraturan umum :
Jika kita mencoba untuk mendapatkan ekspansi dari (a – b)nkita harus mengambil tanda positif dan negatif sebagai alternatif menatap dengan tanda positif untuk suku pertama.
Catatan :
Aturan ini tidak hanya berlaku untuk kekuatan ‘4’. Aturan ini berlaku untuk setiap nilai ‘n’ di (a – b)n.
Untuk mendapatkan ekspansi (a – b)4kita tidak perlu melakukan banyak pekerjaan.
Seperti yang telah kami jelaskan di atas, kita bisa mendapatkan perluasan dari (a + b)4 dan kemudian kita harus mengambil tanda-tanda positif dan negatif sebagai alternatif menatap dengan tanda positif untuk istilah pertama
Jadi, ekspansinya adalah
(a – b)4 =4 – 4a3b + 6a2b2 – 4ab3 + b4
Dengan cara ini, menggunakan segitiga pascal untuk mendapatkan ekspansi binomial dengan eksponen apa pun.
Masalah Terpecahkan
Luaskan binomial berikut menggunakan segitiga pascal :
Masalah 1:
(3x + 4th)4
Solusi:
Sudah, kita tahu
(a + b)4 =4 + 4a3b + 6a2b2 + 4ab3 + b4
Membandingkan (3x + 4y)4 dan (a + b)4kita mendapatkan
a = 3x dan b = 4y
Substitusikan a = 3x dan b = 4y pada pemuaian (a + b)4
(3x + 4th)4
= (3x)4 + 4(3x)3(4 tahun) + 6(3x)2(4 tahun)2 + 4(3x)(4th)3 + (4 tahun)4
= 81x4 + 4(27x3)(4th) + 6(9x2)(16thn2) + 4(3x)(64y3) + 256y4
= 81x4 + 432x3y + 864x2kamu2 + 768xy3 + 256 tahun4
Masalah 2:
(x – 4y)4
Solusi:
Sudah, kita tahu
(a – b)4 =4 – 4a3b + 6a2b2 – 4ab3 + b4
Membandingkan (x – 4y)4 dan (a – b)4kita mendapatkan
a = x dan b = 4y
Substitusikan a = x dan b = 4y dalam ekspansi (a – b)4.
(x – 4y)4 = x4 – 4(x3)(4y) + 6(x2)(4th)2 – 4(x)(4th)3 + (4 tahun)4
= x4 – 16x3y + 6(x2)(16thn2) – 4(x)(64y3) + 256y4
= x4 – 16x3y + 96x2kamu2 – 256xy3 + 256 tahun4
Silakan kirimkan tanggapan Anda ke info@wikitanic.com
Kami selalu menghargai umpan balik Anda.
©Seluruh hak cipta. wikitanic.com