Hello, Selamat datang di wikitanic.com.
Soal cerita diagram Venn dalam pelajaran ini akan menunjukkan kepada Anda bagaimana menggunakan diagram Venn dengan 2 lingkaran untuk menyelesaikan soal yang melibatkan penghitungan.
Soal cerita diagram Venn dengan dua lingkaran
Masalah kata #1
Sebuah survei dilakukan di lingkungan dengan 128 keluarga. Survei mengungkapkan informasi berikut.
- 106 keluarga memiliki kartu kredit
- 73 keluarga berusaha melunasi pinjaman mobil
- 61 keluarga memiliki kartu kredit dan pinjaman mobil
Jawab pertanyaan berikut:
1. Berapa banyak keluarga yang dimiliki hanya sebuah kartu kredit?
2. Berapa banyak keluarga yang dimiliki hanya pinjaman mobil?
3. Berapa banyak keluarga yang tidak memiliki kartu kredit atau pinjaman mobil?
4. Berapa banyak keluarga yang tidak memiliki kartu kredit?
5. Berapa banyak keluarga yang tidak memiliki pinjaman mobil?
6. Berapa banyak keluarga yang memiliki kartu kredit atau pinjaman mobil?
- Biarkan C menjadi keluarga dengan kartu kredit
- Biarkan L menjadi keluarga dengan pinjaman mobil
- Biarkan S menjadi jumlah total keluarga
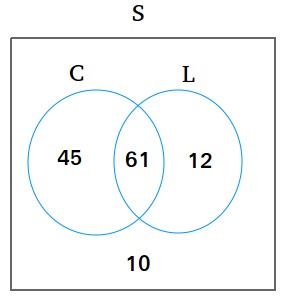
Diagram Venn di atas dapat digunakan untuk menjawab semua pertanyaan tersebut.
Tips cara membuat diagram Venn.
Selalu taruh pertama, di tengah atau di persimpangan, nilai yang ada di kedua himpunan. Misalnya sejak 61 keluarga memiliki kartu kredit dan pinjaman mobil, letakkan 61 di persimpangan sebelum Anda melakukan hal lain.
Di C saja, masukkan 45 sejak 106 – 61 = 45
Di L saja, masukkan 12 sejak 73 – 61 = 12
Di luar C dan L, masukkan 10 karena 128 – 61 – 45 – 12 = 10
Larutan
Ekspresi, “hanya kartu kredit” artinya hanya di C. Angka apa pun di L tidak dapat disertakan.
1. Jumlah keluarga yang hanya memiliki kartu kredit adalah 45. Jangan tambahkan 61 ke 45 karena 61 ada di L.
2. Jumlah keluarga yang hanya memiliki kredit mobil adalah 12.
3. Banyaknya keluarga yang tidak memiliki kartu kredit maupun kredit mobil adalah 10. 10 tidak ada di C maupun L.
4. Jumlah keluarga tanpa kartu kredit ditemukan dengan menjumlahkan semua yang tidak ada di C.
12 + 10 = 22
5. Jumlah keluarga tanpa pinjaman mobil ditemukan dengan menambahkan semua yang tidak ada di L.
45 + 10 = 55
6. Jumlah keluarga dengan kartu kredit atau pinjaman mobil ditemukan dengan menambahkan sesuatu di C saja, di L saja dan di persimpangan C dan L?
45 + 61 + 12 = 118
Masalah kata #2
Sebuah survei yang dilakukan di sebuah sekolah dengan 150 siswa mengungkapkan informasi berikut:
- 78 siswa terdaftar di kelas renang
- 85 siswa terdaftar di kelas bola basket
- 25 terdaftar di kelas renang dan bola basket
Jawab pertanyaan berikut:
1. Berapa banyak siswa yang terdaftar hanya di kelas renang?
2. Berapa banyak siswa yang terdaftar hanya di kelas bola basket?
3. Berapa banyak siswa yang tidak terdaftar di kelas renang atau kelas bola basket?
4. Berapa banyak siswa yang tidak terdaftar di kelas renang?
5. Berapa banyak siswa yang tidak terdaftar di kelas bola basket?
6. Berapa banyak siswa yang terdaftar di kelas renang atau kelas bola basket?
- Misalkan S adalah siswa yang terdaftar di kelas renang
- Misalkan B adalah siswa yang terdaftar di kelas bola basket
- Biarkan E menjadi jumlah total siswa
Menggunakan teknik yang sama seperti di masalah #1kami memiliki diagram Venn berikut
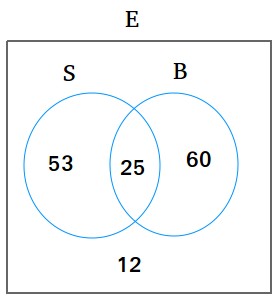
1. Jumlah siswa yang terdaftar hanya pada kelas renang adalah 53 orang
2. Jumlah siswa yang terdaftar hanya di kelas bola basket adalah 60 orang
3. Banyaknya siswa yang tidak mengikuti kelas renang maupun bola basket adalah 12 orang
4. Siswa yang tidak terdaftar di kelas renang terdaftar di kelas bola basket hanya atau tidak terdaftar dalam kedua kegiatan ini. Dengan kata lain, semua yang tidak ada di S.
60 + 12 = 72
5. Siswa yang tidak terdaftar di kelas bola basket hanya terdaftar di kelas renang atau tidak terdaftar di kedua kegiatan ini. Dengan kata lain, segala sesuatu yang tidak ada di B.
53 + 12 = 65
6. Banyaknya siswa yang terdaftar di kelas renang atau bola basket ditemukan dengan menambahkan sesuatu di S saja, di B saja dan di persimpangan S dan B?
53 + 25 + 60 = 138
Soal kata diagram Venn yang rumit dengan dua lingkaran
Masalah kata #3
Dalam survei terhadap 100 orang, 28 orang merokok, 65 orang minum, dan 30 orang tidak. Berapa banyak orang yang melakukan keduanya?
Larutan
- Misalkan K adalah banyaknya orang yang merokok
- Biarkan D menjadi jumlah orang yang minum
- Biarkan E menjadi jumlah total orang
- Biarkan x menjadi jumlah orang yang merokok dan minum
Jika kita membuat diagram Venn, inilah yang kita miliki sejauh ini.
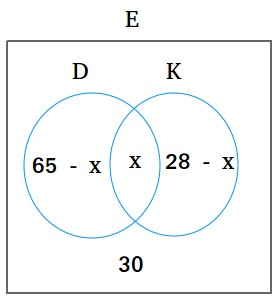
Kita berakhir dengan persamaan berikut untuk memecahkan x.
(65 – x) + x + (28 – x) + 30 = 100
65 – x + x + 28 – x + 30 – 30 = 100 – 30
65 – x + x + 28 – x = 70
65 + 0 + 28 – x = 70
93 – x = 70
Karena 93 – 23 = 70, x = 23
Banyaknya orang yang melakukan keduanya adalah 23 orang.