Hukum Cosinus – Rumus, Bukti, dan Contoh

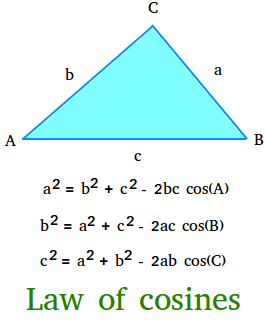
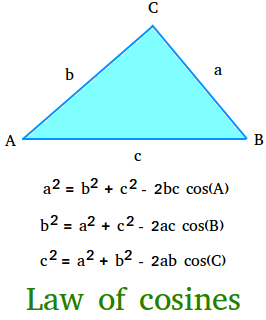
Hukum Cosinus, disebut juga Aturan Cosinus atau Hukum Cosinus, menyatakan bahwa kuadrat sisi sebuah segitiga adalah setara dengan jumlah kuadrat dari dua sisi lainnya dikurangi dua kali perkaliannya dengan kosinus sudut yang disertakan.

Rumus Hukum Kosinus

Kapan Anda harus menggunakan Hukum Kosinus?

Kami menggunakan Hukum Kosinus untuk menyelesaikan segitiga miring atau segitiga apa pun yang bukan segitiga siku-siku. Saat memecahkan segitiga miring, Anda mencoba mencari panjang ketiga sisinya dan ukuran ketiga sudut segitiga miring tersebut.

Memecahkan segitiga SAS atau segitiga Sisi-Sudut-Sisi

Jika dua sisi dan termasuk sudut (SAS) dari segitiga miring diketahui, maka tidak satupun dari tiga rasio dalam Hukum Sinus diketahui. Oleh karena itu, pertama-tama Anda harus menggunakan hukum kosinus untuk mencari sisi ketiga atau sisi yang berhadapan dengan sudut tertentu. Ikuti tiga langkah di bawah ini untuk menyelesaikan segitiga miring.

1. Gunakan Hukum Kosinus untuk mencari sisi yang berhadapan dengan sudut tertentu
2. Gunakan lagi Hukum Sinus atau Hukum Kosinus untuk mencari sudut lain
3. Temukan sudut ketiga dengan mengurangkan ukuran sudut yang diberikan dan sudut yang ditemukan pada langkah 2 dari 180 derajat.

Memecahkan segitiga SSS atau segitiga Sisi-Sisi-Sisi

Jika tiga sisi (SSS) diketahui, menyelesaikan segitiga berarti mencari ketiga sudutnya. Ikuti tiga langkah berikut untuk menyelesaikan segitiga miring.

1. Gunakan hukum kosinus untuk mencari sudut terbesar di hadapan sisi terpanjang
2. Gunakan lagi Hukum Sinus atau Hukum Kosinus untuk mencari sudut lain
3. Temukan sudut ketiga dengan mengurangkan ukuran sudut yang ditemukan pada langkah 1 dan langkah 2 dari 180 derajat.

Contoh yang menunjukkan bagaimana menggunakan Hukum Kosinus

Contoh 1:

Selesaikan segitiga di bawah ini dengan A = 120 derajat, b = 7, dan c = 8.

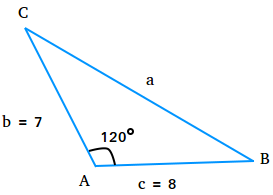
sebuah² = b² + c² – 2bc cos(A)

sebuah² = 7² + 8² – 2(7)(8) cos(120)

sebuah² = 49 + 64 – 2(56)(-0,5)

sebuah² = 113 + 1(56)

sebuah² = 113 + 56

sebuah² = 169

a = √169 = 13

Gunakan Hukum Sinus untuk mencari sudut C

sin C / c = sin A / a

sin C / 8 = sin 120/13

sin C / 8 = 0,866 / 13

sin C / 8 = 0,0666

Kalikan kedua ruas dengan 8

sin C = 0,0666(8)

sin C = 0,536

C = arcsin(0,5328)

C = 32,19

Sudut B = 180 – 120 – 32,19

Sudut B = 27,81

Panjang sisi segitiga adalah 7, 8, dan 13. Besar sudut segitiga adalah 27,81, 32,19, dan 120 derajat.

Contoh #2:

Selesaikan segitiga ABC jika a = 9, b = 12, dan c = 10.

Tidak ada sisi yang hilang. Kita hanya perlu menemukan sudut yang hilang. Karena sudut di depan sisi terpanjang adalah sudut B, gunakan b² = a² + c² – 2ac cos(B) untuk menemukan cos(B).

b² = a² + c² – 2ac cos(B)

12² = 9² + 10² – 2(9)(10) cos(B)

144 = 81 + 100 – 2(90) cos(B)

144 = 181 – 180 cos(B)

144 – 181 = -180 cos(B)

-37 = -180 cos(B)

Bagilah kedua sisi dengan -180

cos(B) = -37 / -180 = 0,205

B = arccos(0,205)

B = 78,17 derajat

Gunakan Hukum Sinus untuk mencari sudut A

sin(A) / a = sin(B) / b

sin(A) / 9 = sin(78,17) / 12

sin(A) / 9 = 0,97876 / 12

sin(A) / 9 = 0,081563

Kalikan kedua ruas dengan 9

sin(A) = 0,081563(9)

sin(A) = 0,734

A = arcsin(0,734)

A = 47,22 derajat

Sudut C = 180 – 78,17 – 47,22

Sudut C = 54,61

Bukti Hukum Kosinus

Untuk membuktikan Hukum Cosinus, letakkan segitiga ABC dalam sistem koordinat persegi panjang seperti yang ditunjukkan pada gambar di bawah ini. Perhatikan bahwa simpul A ditempatkan di titik asal dan sisi c terletak sepanjang sumbu x positif.

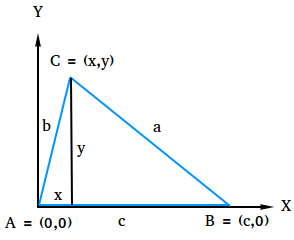
Menggunakan rumus jarak dan titik (x,y) dan (c,0) untuk mencari panjang a.

a = √[(x – c)² + (y – 0)²]

a = √[(x – c)² + y²]

Kotak kedua sisi persamaan

sebuah² = (x – c)² + y²

Sekarang, kita perlu menemukan x dan y dan menggantinya dengan a² = (x – c)² + y²

Dengan menggunakan segitiga, tuliskan ekspresi untuk sin A dan cos A, lalu selesaikan x dan y.

sin(A) = y / b, jadi y = bsin(A)

cos(A) = x / b, jadi x = bcos(A)

sebuah² = (bcos A – c)² + (bsin A)²

sebuah² = b² cos² A – 2bc cos A + c² + b² dosa² SEBUAH

Mengatur kembali ketentuan

sebuah² = b² cos² A + b² dosa² A + c² – 2bc cos A

sebuah² = b²(cos² A+ tanpa² SEBUAH) +c² – 2bc cos A

sebuah² = b²(1) +c² – 2bc cos A sejak cos² A+ tanpa² A = 1

sebuah² = b² + c² – 2bc cos A